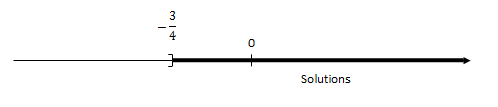L'énoncé
Voici quelques problèmes. Ils sont à votre portée. Prenez bien le temps de les résoudre.
Question 1
Résoudre l'équation suivante \((3x - 5)^2 = (-2x + 7)^2\)
\( (3x - 5)^2 = (-2x + 7)^2\)
\((3x - 5)^2 - (-2x + 7)^2 = 0\)
C'est là que vous utilisez l'identité remarquable : \(a^2 - b^2 = (a - b)(a + b)\)
Ainsi : \([(3x - 5) + (-2x + 7)] [(3x - 5) - (-2x + 7)] = 0 \)
\((3x - 5 - 2x + 7) (3x - 5 + 2x - 7)] = 0\) (Attention au signe « - » devant la parenthèse)
\((x + 2) (5x - 12) = 0\)
C'est une équation-produit nul. Si un produit est nul alors l'un, au moins, des facteurs est nul. Donc :
\(x + 2 = 0\) ou \(5x - 12 = 0\)
\(x = -2\) ou \(5x = 12\)
\(x = -2\) ou \(x = \dfrac{12}{5}\)
\(x = -2\) ou \(x = 2,4\)
-2 et 2, 4 sont les solutions de l'équation.
Le premier réflexe est de tout développer… Vous pouvez toujours essayer.
Et oui, ça donne une équation du second degré … que vous ne savez pas encore résoudre. (Il faudra attendre le lycée.)
Alors si on ne développe pas, il faut tenter autre chose, et là vous n’avez guère le choix : tout mettre du même côté.
\((3x – 5)^2 - (-2x + 7)^2 = 0\)… Ça ne vous rappelle rien ? Mais si bien sûr ! Une « identité remarquable » !
Vous devez aboutir à un produit nul… C’est une équation-produit !
Allez ! C’était la dernière astuce… Maintenant vous vous débrouillez !
Question 2
Aujourd'hui, Rémi a $11$ ans et Luc a $26$ ans. Dans combien d'années, l'âge de Luc sera-t-il le double de celui de Rémi ?
La deuxième équation !
Aujourdhui, Rémi a $11$ ans et Luc a $26$ ans. Dans combien d'années, l'âge de Luc sera-t-il le double de celui de Rémi ?
Soit \(x\) le nombre d'années qui vont s'écouler avant que l'âge de Luc soit le double de celui de Rémi.
Dans \(x\) années Rémi aura \(11 + x\) ans et Luc aura \(26 + x\) ans.
Donc on cherche à trouver \(x\) tel que \((26 + x) = 2 \times (11 + x)\)
\(26 + x = 22 + 2x\)
\(26 - 22 = 2x - x\)
\(4 = x\)
Dans $4$ ans, l'âge de Luc sera le double de celui de Rémi.
Vérification : Rémi aura $15$ ans et Luc aura $30$ ans : cela fonctionne !
Ce problème sera résolu grâce à une équation. Construisons la !
Soit \(x\) le nombre d’années qui vont s’écouler avant que l’âge de Luc soit le double de celui de Rémi.
Par conséquent, dans \(x\) années Rémi aura \(11 + x\) ans et Luc aura \(26 + x\) ans.
Et donc on cherche à trouver \(x\) tel que \((26 + x) = 2 \times (11 + x)\)
Question 3
La première inéquation !
Résoudre l'inéquation suivante \(-3x + \dfrac{13}{4} < 2x + 7\) et représenter graphiquement les solutions.
Résoudre l'inéquation suivante \(-3x + \dfrac{13}{4} < 2x + 7\) et représenter graphiquement les solutions.
\(-3x - 2x < 7 - \dfrac{13}{4}\)
\(- 5x < \dfrac{28}{4} - \dfrac{13}{4}\)
\(- 5x < \dfrac{15}{4}\)
Attention, on divise à droite et à gauche par -5 qui est un nombre négatif, il faut donc que vous n'oubliez pas d'inverser le sens de l'inégalité !
\(\dfrac{-5x}{-5} > \dfrac{15}{-5 \times 4}\)
\(x>-\dfrac{15}{20}\)
\(x>-\dfrac{3}{4}\)
Les solutions sont donc les nombres strictement supérieurs à \(-\dfrac{3}{4}\)
Il faut regrouper les termes en \(x\) et les termes constants.
Si vraiment vous détestez les fractions, vous pouvez aussi essayer de vous débarrasser du dénominateur 4.
Pour cela, il faudrait tout multiplier par 4.
Le symbole « < » signifie « strictement inférieur à ».
Lorsque le crochet est « tourné » vers les solutions, cela signifie que le nombre en question en fait partie.
Question 4
La deuxièmee inéquation !
On donne l'inéquation suivante \( -5 (1 - 2x) < 2 (4x + 3)\)
Avec \(x\) entier naturel strictement positif.
Démontrer que la somme des solutions de cette inéquation est égale à $15$.
On résout l'inéquation : \(-5 (1 - 2x) < 2 (4x + 3)\)
\(-5 + 10x < 8x + 6\)
\(10x - 8x < 6 + 5\)
\(2x < 11\)
\(x < 5,5\)
Or \(x\) est un entier naturel strictement positif.
Donc les solutions de cette inéquation sont : $1, 2, 3, 4$ et $5$.
Et leur somme est égale à \(1 + 2 + 3 + 4 +5 = 15\).
Cette histoire de « somme de solutions » est assez bizarre… On verra plus tard… Commencez par résoudre l’inéquation.
Développez et regroupez les termes de la même « famille » de chaque côté.
Vous devez arriver à \(x < 5,5\)… Or d’après la consigne x est un entier strictement positif. Or des entiers strictement positifs inférieurs à 5,5 il n’y en a pas beaucoup.
1, 2, 3, 4 et 5.
Or, \(1 + 2 + 3 + 4 + 5 =\)….
Question 5
Résoudre le système : \(\left\{ \begin{array}{rcl} \dfrac{2}{3} x+ \dfrac{3}{4} y=51,5 \\ \dfrac{5}{6} x+\dfrac{2}{5} y=41,8 \end{array} \right. \)
Résoudre le système : \(\left\{ \begin{array}{rcl} \dfrac{2}{3} x+ \dfrac{3}{4} y=51,5 \\ \dfrac{5}{6} x+\dfrac{2}{5} y=41,8 \end{array} \right. \)
On multiplie l'équation n°1 par $12$ (c'est le dénominateur commun aux deux fractions de cette équation).
On multiplie l'équation n°2 par $30$ (c'est le dénominateur commun aux deux fractions de cette équation).
Il vient : \(\left\{ \begin{array}{rcl} 8 x+ 9 y=618 \\ 25 x+12 y=1254 \end{array} \right. \)
Et maintenant on soustrait la 1ère équation à la seconde de façon à éliminer le terme en y (tout en gardant un coefficient positif pour le terme en \(x\)).
Ce qui donne :
\(75x - 32 x + 36y - 36y = 3 762 2 472\)
\(43x = 1 290\)
\(x = \dfrac{1 290}{43}\)
\(x = 30\)
On remplace \(x\) dans l'équation n°1 (ou dans la n° 2, peu importe). Et on a :
\(8 \times 30 + 9y = 618\)
\(9y = 618 - 240\)
\(9y = 378\)
\(y = 42\)
Le couple \((30 ; 42)\) est la solution de ce système.
Ouh la la ! Ça en fait des fractions... Et si vous commenciez par les éliminer ?
Par exemple en multipliant l’équation n°1, par le dénominateur commun des deux fractions de cette équation. Et pareil pour l’équation n°2.
Pour l’équation n°1, il faut que vous multipliez par 12.
Pour l’équation n°2, il faut que vous multipliez par 30.
Le système devient : \(\left\{ \begin{array}{rcl} 8 x+ 9 y=618 \\ 25 x+12 y=1254 \end{array} \right. \)
Substitution ou combinaison ? Allez ! C’était la dernière astuce… Maintenant vous vous débrouillez !