Fiche de cours
I. Equation de la trajectoire
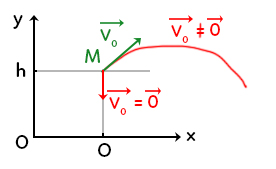
Sur ce schéma, nous avons un point $M$ d’abscisse $0$ et d’altitude $h.$ L’axe $z$ n’est pas représenté car nous savons déjà que le point reste toujours dans la direction $z=0.$
Il y a deux situations :
- Si la vitesse initiale est différente de zéro, c'est un mouvement parabolique.
- Si la vitesse initiale est égale au vecteur nul, c'est une chute libre.
Pour rappel, ce qui a été vu dans les équations horaires : l’expression du vecteur position $ \overrightarrow{OM}(t) = \begin{bmatrix} v_0 \times \cos(\alpha)\times t \\ -\dfrac{1}{2}\times g \times t^2+ v_0 \times \sin(\alpha)\times t+h \end{bmatrix}$
Dans un premier temps, nous allons isoler le temps (t) grâce à l’équation 1. Ainsi on a :
$X(t) = v_0\times \cos(\alpha)\times t $ -> $t = \dfrac{x(t)}{ v_0\times \cos(\alpha) }$
Cela est vrai si $v_0$ est différent de zéro, sinon nous sommes dans une forme indéterminée (division par zéro).
Maintena
