Fiche de cours
Étape 4 : l’équation de la trajectoire d’un mouvement
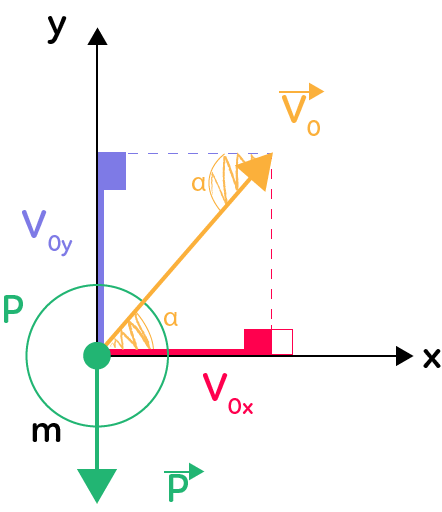
Les équations horaires ont été déterminées : $\overrightarrow{OG} \left\{
\begin{array}{ccc}
x & = & v_0 \times \cos(\alpha)\times t \\
y & = & -\dfrac{1}{2} \times gt^2 + v_0 \times \sin(\alpha) \times t \\
\end{array}
\right.$
Il est désormais possible d’établir l’équation de la trajectoire, permettant de suivre le trajet de la balle, et s’écrivant de la forme $y = f(x)$, où $f$ est la fonction indépendante du temps qu’il faut déterminer.
Afin d’éliminer le temps au profit des autres paramètres $x$ et $y$, on détermine la valeur de $t$ en fonction de $x$ : $t = \dfrac{x}{v_0\times \cos(\alpha)}$.
On remplace ensuite cette nouvelle valeur de $t$ dans l’expression de $y$ :
$y = -\dfrac{1}{2} \times g \times \left( \dfrac{x}{v_0\times \cos(\alpha)} \right)^2 + v_0 \times \sin(\alpha) \times \dfrac{x}{v_0\times \cos(\alpha)}$
On simplifie alors e
