Fiche de cours
Étape 3 : la vitesse du satellite
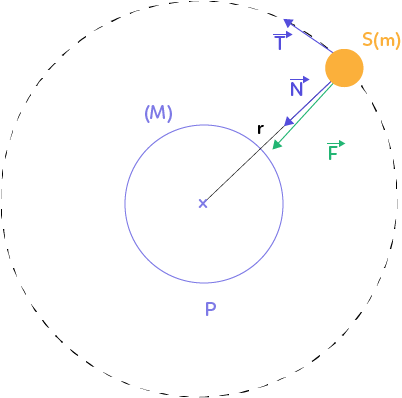
L’application de la seconde loi de Newton au satellite a permis de trouver la relation vectorielle suivante :
$\overrightarrow{a} = \dfrac{G M}{r^2} \overrightarrow{N}$ où $G$ est la constante universelle de gravitation, $M$ la masse de la planète, $r$ la distance séparant les centres du satellite et de la planète et $\overrightarrow{N}$ est un vecteur unitaire normal à la trajectoire.
En supposant le mouvement du satellite circulaire, on peut réécrire la formule du vecteur accélération : $\overrightarrow{a} = a_t \overrightarrow{T} + a_n \overrightarrow{N}$.
De plus, pour un mouvement circulaire, on dispose également de la relation suivante :
$\overrightarrow{a} = \dfrac{\text{d}v}{\text{dt}}\overrightarrow{T} + \dfrac{v^2}{r} \overrightarrow{N}$ où $v = \| \overrightarrow{v} \|$ et $\overrightarrow{v}$ est le vecteur vitesse du satellite.
En combinant les différents résultats, on obtient :
$ \dfrac{G M}{r^2} \overrightarrow{N} = \dfrac{\text{d}v}{\text{dt}}\overrightarrow{T} + \dfrac{v^2}{r} \
