Fiche de cours
Étape 2 : La deuxième loi de Newton
Le référentiel est galiléen, permettant ainsi d’appliquer les lois de Newton, et en particulier la seconde loi de Newton.
Cette dernière stipule que :
$\sum \overrightarrow{F_{ext}} = m \times \overrightarrow{a_{satellite}} = \dfrac{\text{d}\overrightarrow{p}}{\text{dt}}$,
ou encore que la somme des forces extérieures agissant sur le satellite est égale au produit de la masse du satellite par l’accélération de ce dernier ou à la dérivée de la quantité de mouvement du satellite par rapport au temps.
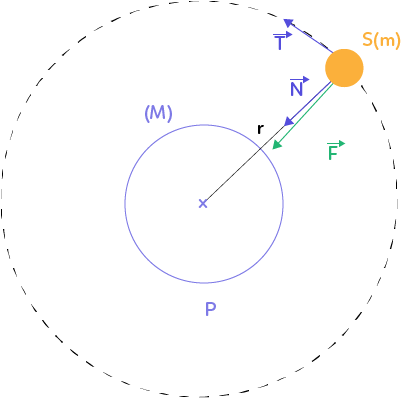
Ici, la seule force que subit le satellite est la force d’interaction gravitationnelle. Cette force est dirigée par la droite reliant les centres du satellite et de la planète et orientée du satellite vers la planète. La distance entre les deux centres est notée $r$.
Ainsi on trouve $\overrightarrow{F_G} = m \times \overrightarrow{a}$ que l’on peut réécrire dans la base $\left (\over
