L'énoncé
Par la suite, s’il est à l’heure un jour, la probabilité qu’il soit à l’heure le lendemain est de 30%. S’il est en retard un jour, la probabilité qu’il soit en retard le lendemain est de 50%.
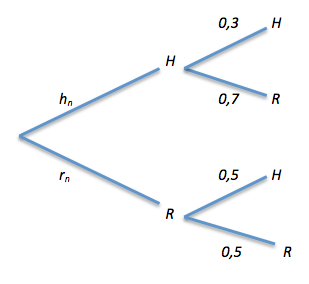
Soit \(h_n\) et \(r_n\) les probabilités que Bertrand soit respectivement à l’heure et en retard le n-ième jour.
On pose, pour tout entier naturel n, \(U_n = \begin{pmatrix} h_n \\ r_n \end{pmatrix} \) et \(U_0 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \).
Question 1
Exprimer \(h_{n+1}\) et \(r_{n+1}\) en fonction de \(h_{n}\) et \(r_{n}\).
On note $R$ et $H$ les évènements « Etre en retard » et « Etre à lheure ».
Représentons la situation par un arbre pondéré : 
Daprès la formule de probabilité totale, on a :
\(h_{n+1} = 0,3h_n + 0,5r_n\)
\(r_{n+1} = 0,7h_n + 0,5r_n\)
D’après l’arbre, il y a deux possibilités pour obtenir \(h_{n+1}\) et \(r_{n+1}\), quelle est la probabilité de chacune ?
Utilisez la formule des probabilités totales pour conclure.
\(B_1, B_2, ...., B_N\) est une partition de \(\Omega\). Alors pour tout événement A, on a :
\(P(A) = P(A \cap B_1) + P(A \cap B_2) + ........ + P(A \cap B_n)\).
Question 2
En déduire la matrice carrée A dordre 2 telle que \(U_{n+1} = AU_n\)
\(U_{n+1} = AU_n\)
\(U_{n+1} = \begin{pmatrix} 0,3 & 0,5 \\ 0,7 & 0,5 \end{pmatrix} \begin{pmatrix} h_n \\ r_n \end{pmatrix} \)
La question débute par la formule magique « En déduire » ! Avez-vous pensé à utiliser le résultat de la question précédente ?
Il ne reste plus qu’à écrire le système sous forme matricielle. Un doute sur la méthode ? Revoyez le rappel vidéo via les prérequis.
Question 3
Démontrer que pour tout entier naturel n, \(U_n = A^nU_0\)
Démontrons par récurrence que pour tout entier naturel n, \(U_n = A^nU_0\).
Initialisation : pour n=0 : \(U_0 = IU_0\).
Hérédité :
On suppose qu'il existe un réel k tel que \(U_k = A^kU_0\).
\(U_{k+1} = AU_k\)
\(U_{k+1} = AA^kU_0\)
\(U_{k+1} = A^{k+1}U_0\)
Donc pour tout entier naturel n, \(U_n = A^nU_0\)
La récurrence se fait en 2 étapes : l'initialisation et l'hérédité.
Initialisation : est-ce vrai pour n = 0 ?
Hérédité : Si l'assertion est vrai au rang n, montrons qu'elle est vraie aussi au rang n + 1.
Question 4
Démontrer que pour tout entier naturel $n$, \(A^n = \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} + \left(\dfrac{-1}{5}\right)^n \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix}\)
Démontrons par récurrence que pour tout entier naturel n, \(A^n = \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^n \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix}\)
Initialisation : pour n=0, on a
\(A^0 = \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} + \dfrac{-1}{5} \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix}\)
\(A^0 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\)
\(A^0 = I\)
Hérédité :
On suppose qu'il existe un entier naturel $k$ tel que \(A^k= \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^k \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix}\).
On a :
\(A^{k+1}= A^kA\) \(A^{k+1} = \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^k \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix} \begin{pmatrix} 0,3 & 0,5 \\ 0,7 & 0,5 \end{pmatrix}\)
\(A^{k+1}= \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^{k+1} \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix}\)
Donc pour tout entier naturel n,
\(A^n= \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^n \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix}\)
Le plus délicat ici est de maîtriser les calculs sur les matrices et les expressions à rallonge. Prenez votre temps.
N'oubliez pas : \(A^{n+1} = A^nA\). On connait A et on suppose \(A^n\).
Question 5
En déduire lexpression de \(U_n\) en fonction de n.
\(U_n = A^nU_0\)
\(U_n = \left\lbrack \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^n \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix} \right\rbrack \begin{pmatrix} 1 \\ 0 \end{pmatrix}\)
\(U_n = \dfrac{1}{12} \begin{pmatrix} 5 & 5 \\ 7 & 7 \end{pmatrix} \begin{pmatrix} 1 \\0 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^n \times \dfrac{1}{12} \begin{pmatrix} 7 & -5 \\ -7 & 5 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \)
\(U_n = \dfrac{1}{12} \begin{pmatrix} 5 \\ 7 \end{pmatrix} +\left(\dfrac{-1}{5}\right)^n \times \dfrac{1}{12} \begin{pmatrix} 7 \\ -7 \end{pmatrix}\)
Question 6
A long terme, quelle est la probabilité que Bertrand soit à l'heure ?
On a :\(U_n = \begin{pmatrix} h_n \\ r_n \end{pmatrix} \)
Donc à l'aide de la question précédente , \(h_n = \displaystyle\dfrac{5}{12} +\left(\dfrac{-1}{5}\right)^n \dfrac{7}{12}\)
D'où :
\(\displaystyle\lim_{n \to +\infty} h_n = \dfrac{5}{12}\)
\(\displaystyle\lim_{n \to +\infty} h_n \approx 0,42\)
A long terme, la probabilité que Bertrand soit à l'heure est de 42%.
Il faut penser à calculer la limite de la suite \((h_n)\) !
\(h_n = \dfrac{5}{12} + (\dfrac{-1}{5})^n \dfrac{7}{12}\).
On connaît la limite de \((\dfrac{-1}{5})^n\).