Fiche de cours
Loi exponentielle - Propriétés
Propriétés
On considère une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda>0$.
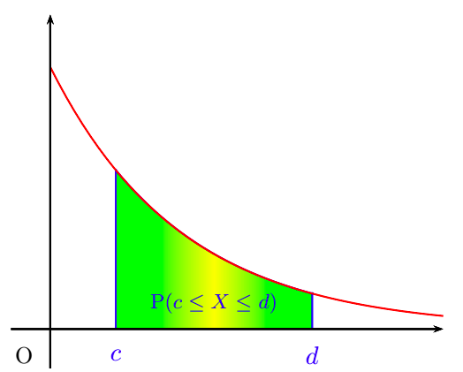
Si $X\in [c;d]$, on a:
\( \displaystyle P(c\leqslant X \leqslant d)= \int \limits_{c}^{d}\lambda e^{-\lambda t}dt= \left[-e^{-\lambda t}\right]_c^d =e^{-\lambda c}-e^{-\lambda d} \)
Pour tout réel $a>0$ :
\( \displaystyle P( X \leqslant a)= \int \limits_{0}^{a}\lambda e^{-\lambda t}dt= 1 -e^{-\lambda a}\)
Par l'événement contraire, on a:
\( \displaystyle P( X \geqslant a)= 1-P(X\leqslant a) = e^{-\lambda a}\).
Espérance mathématique: \( \displaystyle E(X)=\frac{1}{\lambda}\)
Théorème
Une loi exponentielle est une loi de durée de vie sans vieillissement c'est-à-dire:
Pour tous $t>0$ et $h>0$, on a :
\( \displaystyle P_{ X \geqslant t}( X \geqslant t+h) = P( X \geqslant h) = e^{-\lambda h}\)
Exemple
La durée de vie, en année, d'un composant électronique est une variable aléatoire not&e
