Fiche de cours
Un rappel de cours sur la loi exponentielle sur [0 ; +infini[ en Maths TS.
Loi exponentielle sur $[0 ; +\infty[$
Définition
Soit $\lambda>0$ un paramètre réel.
Une variable aléatoire $X$ suit une loi exponentielle de paramètre $\lambda>0$ si et seulement si la fonction densité $f$ de cette loi est définie sur $[0 ; +\infty[$ par:
\( \displaystyle f(x)= \lambda e^{-\lambda x}\)
$f$ est continue et positive et \( \displaystyle \lim_{x \rightarrow +\infty}\int \limits_{0} ^{x}f(t)dt=1 \)
Ainsi, $f$ est bien une densité de probabilité.
Voici la représentation graphique du cas $\lambda=2$
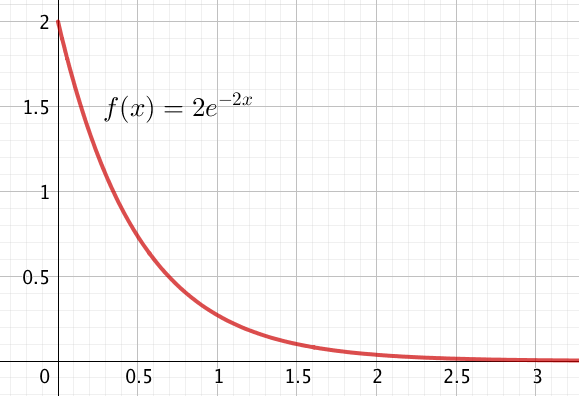
Propriétés
La fonction de répartition vaut:
\( \displaystyle P(X \leqslant x) = \int \limits_{0}^{x}\lambda e^{-\lambda t}dt=\left[-e^{-\lambda t}\right]_0^x \) ou encore :
\( \displaystyle P(X \leqslant x) = 1-e^{-\lambda x} \)
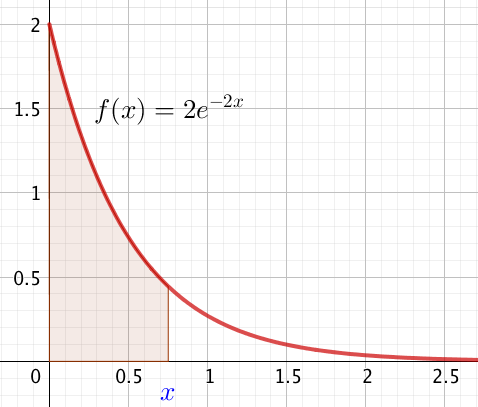
En
