L'énoncé
Soit \(X\) une variable aléatoire continue de densité \(f\) définie sur \(\mathbb{R}\) par :
\( f(x) = \left\{ \begin{array}{ll} 1 + x \;\;\text{ si } -1 \leq\ x < 0\\ 1 - x\;\;\text{ si } 0 \leq\ x \leq 1 \\ 0\;\;\text{ sinon } \end{array} \right. \)
On désire calculer \(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right)\)
Question 1
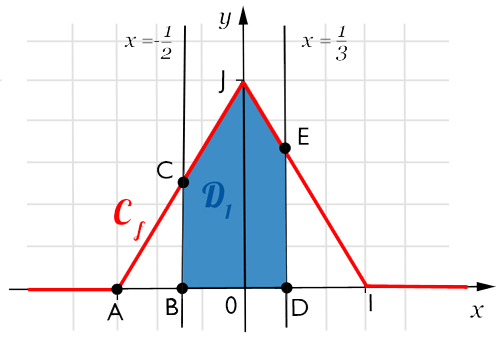
Représenter \(f\) dans un repère orthogonal \((O, I, J)\).
La fonction est représentée par la ligne rouge ci-dessous.
Normalement, cela ne devrait plus vous poser de problème depuis le collège...
Procédez par étape en suivant chaque intervalle.
Question 2
Colorier le domaine correspondant à la probabilité que l'on souhaite calculer.
L'aire du domaine est représentée en bleu ci-dessous.
Par définition, \(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right)\) correspond à l’aire sous la courbe représentative de \(f\) entre \(x = -\dfrac{1}{2}\) et \(x = \dfrac{1}{3}\).
Question 3
Déterminer, grâce à des calculs d'aires, \(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right)\).
Soit \(D_1\) le domaine représentant \(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right)\).
Soient les points \(A(-1,0);\; B\left(-\dfrac{1}{2}, 0\right);\; C\left(-\dfrac{1}{2}, \dfrac{1}{2}\right);\; D\left(\dfrac{1}{3}, 0\right);\; E\left(\dfrac{1}{3}, \dfrac{2}{3}\right)\).
On a alors :
\(A_{(D_1)} = A_{(AIJ)} - A_{(ABC)} - A_{(EDI)}\)
\(A_{(D_1)} = 1 - \dfrac{1}{8} - \dfrac{2}{9}\)
\(A_{(D_1)} = \dfrac{47}{72}\)
Ainsi : \(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right) \approx 0,65\)
Vous devez d’abord nommer des points particuliers, par exemple :
\(A(-1,0);\; B\left(-\dfrac{1}{2}, 0\right);\; C\left(-\dfrac{1}{2}, \dfrac{1}{2}\right);\; D\left(\dfrac{1}{3}, 0\right);\; E\left(\dfrac{1}{3}, \dfrac{2}{3}\right)\)
L’aire du domaine recherché est donc égale au triangle \(AIJ\) auquel il faut soustraire les aires des triangles \(ABC\) et \(DEI\).
Question 4
Retrouver ce résultat par un calcul dintégrale.
Sur \(\left[-\dfrac{1}{2},0\right]\), \(f(x) = 1 + x\) et sur \(\left[0, \dfrac{1}{3}\right]\), \(f(x) = 1 -x\).
Donc :
\(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right) = \displaystyle\int_{-\frac{1}{2}}^0 (1 + x) dx + \displaystyle\int_{0}^{\frac{1}{3}} (1-x) dx\)
\(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right) =\left[x + \dfrac{x^2}{2}\right]_{-\frac{1}{2}}^0 + \left[x - \dfrac{x^2}{2}\right]_{0}^{\frac{1}{3}}\)
\(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right) = \dfrac{1}{2} - \dfrac{1}{8} + \dfrac{1}{3} - \dfrac{1}{18}\)
\(P\left(-\dfrac{1}{2} \leq X \leq \dfrac{1}{3}\right) = \dfrac{47}{72} \approx 0,65\)
Attention ! La fonction étant définie par morceaux, il faut donc effectuer une somme d’intégrales et définir les bonnes bornes.