Fiche de cours
Loi uniforme sur un intervalle $[a;b]$
Définition
$X$, une variable aléatoire suit une loi uniforme sur $[a;b]$ si et seulement si la fonction de densité de probabilité est :
\( \displaystyle f(x)=\frac{1}{b-a}\).
On vérifie que \( \displaystyle \int \limits_a^{b}f(x)dx=1\).
Propriétés
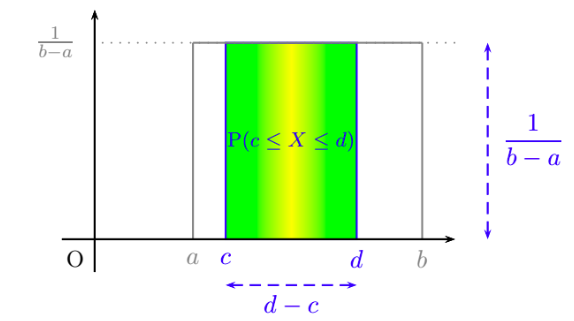
Pour tout intervalle $[c;d]$ inclus dans $[a;b]$, on a:
\( \displaystyle P(c\leqslant X \leqslant d)=\frac{d-c}{b-a}\).
Exemple
1) On choisit un nombre réel au hasard dans l'intervalle $[0 ;5]$. On note $X$ la variable aléatoire égale au nombre choisi.
a)Quelle est la probabilité que ce nombre soit supérieur à 4 ?
b)Compris entre $e$ et $\pi$ ?
Correction
1 a) $X$ suit la loi uniforme sur $[0;5]$. La probabilité que ce nombre soit supérieur à 4 est :
$P(X > 4) = P( 4 < X\leq 5)=\displaystyle\frac{5-4}{ 5-0}=\displaystyle\frac{1}{ 5}$
1 b) La probabilité que ce nombre soit compris entre $e$ et $\pi$ est :
$\displaystyle P(e \leqslant
