Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Lois de probabilité continues
Définition : Densité de probabilité sur un intervalle $[a;b]$
Soit $f$ une fonction continue et positive sur un intervalle $[a;b]$.
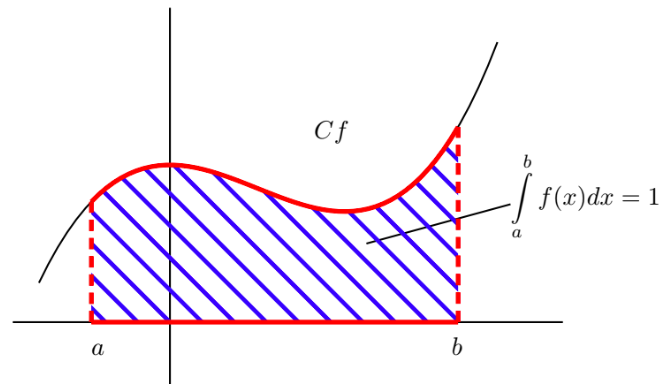
$f$ est une densité de probabilité sur $[a;b]$ si et seulement si :
$ \displaystyle \int \limits_a^{b}f(x)dx=1$
Exemple
Soit $ \displaystyle f(x)=\frac{2}{x^2}$ définie sur $[1 ; 2]$.
Cette fonction $f$ est-elle une densité de probabilité ?
Correction
$f$ est continue et positive sur $[1;2]$. On intègre la fonction entre $1$ et $2$:
\( \displaystyle \int \limits_{1} ^{2}\frac{2}{x^2} dx=\left[ -\frac{2}{x}\right]_{1}^2\)
\( \displaystyle \int \limits_{1} ^{2}\frac{2}{x^2} dx= -\frac{2}{2}+\frac{2}{1} = 1\)
On a donc: \( \displaystyle \int \limits_{1} ^{2} f(x) dx= 1\)
Cette intégrale vaut $1$ donc la fonction $f$ est bien une densité de probabilité sur $[1;2]$.
