Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Positions relatives des courbes
On trace les trois courbes représentatives des fonctions $x \mapsto x$, $x \mapsto \ln(x)$ et $x \mapsto e^x$.
Graphiquement, on remarque que la courbe représentative de la fonction exponentielle est au dessus de la courbe de la fonction $x \mapsto x$, elle même au dessus de la courbe représentative de la fonction logarithme népérien.
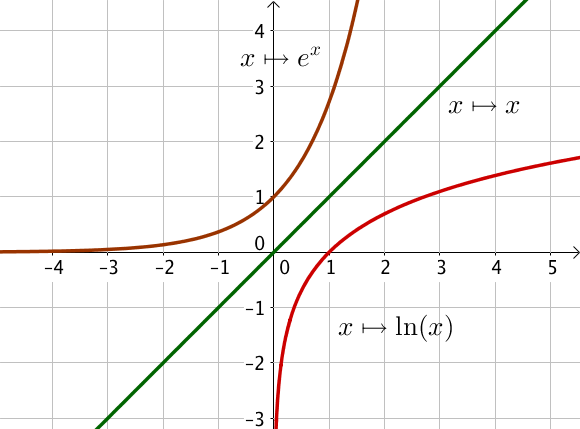
On peut alors en déduire l'inégalité suivante, à connaitre, et qui se retrouve facilement à l'aide d'un graphique :
Pour $x \in ]0; +\infty[$, on a :
$\ln(x) \leq x \leq e^x$.
On remarquera que cette inégalité n'est vraie que pour $x \in ]0; +\infty[$ car le logarithme népérien n'est pas défini pour des valeurs de $x$ négatives.
