Fiche de cours
Outil pour trouver un point d'inflexion
Théorème :
Soit $f$ une fonction définie sur $]a; b[$ telle que $f''$ existe sur $]a; b[$ et $x_0$ un point de l'intervalle $]a; b[$,
si $f''$ s'annule en $x_0$, en changeant de signe alors le point $M_0(x_0, f(x_0))$ est un point d'inflexion.
Exemple :
Soit $f$ la fonction définie par
$f(x) = x^3 - 2x^2 + x$ pour tout réel $x$,
on cherche d'éventuels points d'inflexion.
Pour cela, on calcule tout d'abord $f'$ qui existe car $f$ est polynomiale.
Pour tout $x \in \mathbb{R}, \ f'(x) = 3x^2 - 4x + 1$.
De même, $f'$ est dérivable sur $\mathbb{R}$ car c'est une fonction polynomiale : $f''$ existe donc et
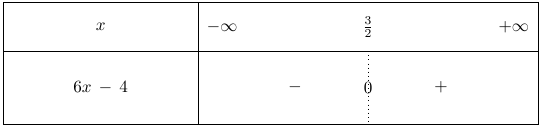
$f''(x) = 6x - 4$.
Pour trouver un point d'inflexion, on cherche à présent une valeur de $x$ pour laquelle la dérivée seconde s'annule et change de signe.
Soit $x \in \mathbb{R}, \ f''(x) = 0 \iff 6x - 4 = 0 \iff x = \dfrac{4}{6} \iff x = \dfrac{2}{3}$.
La dérivée s'annule donc en $x = \dfrac{2}{3}$.
On dresse alors le tableau de signe de $f''(x)$ pour tout réel $x$.