L'énoncé
Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Soient $\overrightarrow{AB} \left ( \begin{array}{c} 1 \\ 2 \\ -3 \end{array} \right )$, $\overrightarrow{AC}\left ( \begin{array}{c} 2 \\ -1 \\ -1 \end{array} \right )$, et $\overrightarrow{AD}\left ( \begin{array}{c} -1 \\ 1 \\ 0 \end{array} \right )$ trois vecteurs de l'espace.
$\overrightarrow{AB} = 5 \overrightarrow{AC} + 3 \overrightarrow{AD} $
$\overrightarrow{AB} = 3 \overrightarrow{AC} + 5 \overrightarrow{AD} $
$\overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{AD} $
On vérifiera pour chaque coordonnée l'égalité.
Question 2
Soient $\overrightarrow{AB} \left ( \begin{array}{c} 3 \\ 2 \\ 1 \end{array} \right )$, $\overrightarrow{AC}\left ( \begin{array}{c} -2 \\ 3 \\ -1 \end{array} \right )$, et $\overrightarrow{AD}\left ( \begin{array}{c} -1 \\-2 \\ 4 \end{array} \right )$ trois vecteurs de l'espace,
$\overrightarrow{AB} = -\dfrac{4}{7} \overrightarrow{AC} -\dfrac{13}{7} \overrightarrow{AD} $
$\overrightarrow{AB} = \dfrac{13}{7} \overrightarrow{AC} + \dfrac{4}{7} \overrightarrow{AD} $
$\overrightarrow{AB}$, $\overrightarrow{AC}$ et $\overrightarrow{AD} $ ne sont pas coplanaires.
En effet,
Soient $a$ et $b$ deux réels,
$\overrightarrow{AB} = a \overrightarrow{AC} + b \overrightarrow{AD} $
$\iff \left \{ \begin{array}{rlc} 3 &=& -2a - b \\ 2 &= & 3a -2b \\ 1 &= &a + 4b \end{array} \right. $
$\iff \left \{ \begin{array}{rlc} 3 &= &-2a - b \\ -4 &= & 7a \\ 1 &= & a + 4b \end{array} \right. $
$\iff \left \{ \begin{array}{rlc} 3 &=& -2a - b \\ a &= & -\dfrac{4}{7} \\ 1 &= & a + 4b \end{array} \right. $
$\iff \left \{ \begin{array}{rlc} 3 -\dfrac{8}{7} &= & - b \\ a &= & -\dfrac{4}{7} \\ 1 &= & a + 4b \end{array} \right. $
$\iff \left \{ \begin{array}{rlc} b&= & -\dfrac{13}{7} \\ a &= & -\dfrac{4}{7} \\ 1 &= & -\dfrac{4}{7} - 4 \times \dfrac{13}{7} \end{array} \right. $
Or $-\dfrac{4}{7} - 4 \times \dfrac{13}{7} = -8 \neq 1$
Donc $\overrightarrow{AB}$, $\overrightarrow{AC}$ et $\overrightarrow{AD} $ ne sont pas coplanaires.
On vérifiera pour chaque coordonnée l'égalité.
Question 3
Quels couples de vecteurs sont coplanaires ?
$\overrightarrow{AB} \left ( \begin{array}{c} 2 \\ -8 \\ 2 \end{array} \right )$, $\overrightarrow{AC}\left ( \begin{array}{c} 2 \\ 3 \\ 1 \end{array} \right )$, et $\overrightarrow{AD}\left ( \begin{array}{c} -3 \\2 \\ -1 \end{array} \right )$
En effet,
Soient $a$ et $b$ deux réels,
$\overrightarrow{AB} = a \overrightarrow{AC} + b \overrightarrow{AD} $
$\iff \left \{ \begin{array}{rcl}2 &=& 2a - 3b \\ -8 &=& -3a +2b \\ 2 &=& a - b \end{array} \right. $
$\iff \left \{ \begin{array}{rcl}2 &=& 2a - 3b \\ -4 &=& -a \\ 2 &=& a - b \end{array} \right. $
$\iff \left \{ \begin{array}{rcl}-6 &=& - 3b \\ a&=&4 \\ 2 &=& a - b \end{array} \right. $
$\iff \left \{ \begin{array}{rcl}-b &=& 2 \\ a&=&4 \\ 2 &=& 4 - 2 \end{array} \right. $
$\iff \left \{ \begin{array}{rcl}-b &=& 2 \\ a&=&4 \\ 2 &=& 2 \end{array} \right. $
$\overrightarrow{AB} \left ( \begin{array}{c} 2 \\ -8 \\ 2 \end{array} \right )$, $\overrightarrow{AC}\left ( \begin{array}{c} 2 \\ 3 \\ 1 \end{array} \right )$, et $\overrightarrow{AD}\left ( \begin{array}{c} -3 \\2 \\ 0 \end{array} \right )$
$\overrightarrow{AB} \left ( \begin{array}{c} -4 \\ -3 \\ -2 \end{array} \right )$, $\overrightarrow{AC}\left ( \begin{array}{c} -2 \\1 \\ 0 \end{array} \right )$, et $\overrightarrow{AD}\left ( \begin{array}{c} -1 \\ 3 \\ 1 \end{array} \right )$/
En effet,
Soient $a$ et $b$ deux réels,
$\overrightarrow{AB} = a \overrightarrow{AC} + b \overrightarrow{AD} $
$\iff \left \{ \begin{array}{rcl}-4 &=& -2a - b \\ -3 &=& a + 3b \\ -2 &=& b \end{array} \right. $
$\iff \left \{ \begin{array}{rcl}-4 &=& -2a +2 \\ -3 &=& a + 3b \\ b &=& -2 \end{array} \right. $
$\iff \left \{ \begin{array}{rcl}a &=& 3 \\ -3 &=& a + 3b \\ b &=& -2 \end{array} \right. $
$\iff \left \{ \begin{array}{rcl}a &=& 3 \\ -3 &=& 3 - 3 \times 2 \\ b &=& -2\end{array} \right. $
$\iff \left \{ \begin{array}{rcl}a &=& 3 \\ -3 &=& -3 \\ b &=& -2 \end{array} \right. $
On cherchera deux réels $a$ et $b$ tels que $\overrightarrow{AB} = a \overrightarrow{AC} + b \overrightarrow{AD} $
Question 4
Soit $ABCD$ un tétraèdre et $M$ milieu de $[BC]$,
Quels couples de vecteurs sont coplanaires ?
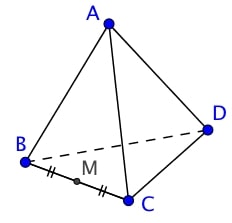
$\overrightarrow{DB}$, $ \overrightarrow{DC}$, $ \overrightarrow{DA} $
$\overrightarrow{BD}$, $ \overrightarrow{DC}$, $ \overrightarrow{MC} $
En effet, les 4 points appartiennent au plan $(BCD)$, les vecteurs associés à ces points sont donc coplanaires.
$\overrightarrow{AC}$, $ \overrightarrow{CD}$, $ \overrightarrow{MB} $
On regardera si les vecteurs appartiennent à un même plan
Question 5
Soit $ABCDEFGH$ un cube,
Donner le ou les vecteurs qui sont une combinaison linéaire de $\overrightarrow{DH}$ et $\overrightarrow{ED}$
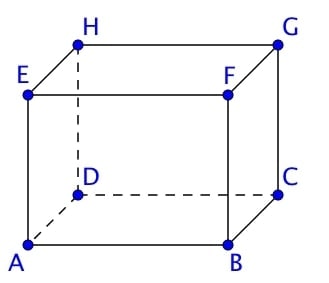
$\overrightarrow{EA}$
En effet, le point $A$ appartient au plan forme par les vecteurs $\overrightarrow{DH}$ et $\overrightarrow{ED}$ et le point $D$, donc $\overrightarrow{EA}$ est coplanaire à $\overrightarrow{DH}$ et $\overrightarrow{ED}$ : $\overrightarrow{EA}$ est donc une combinaison linéaire des deux précédents.
$\overrightarrow{GA}$
$\overrightarrow{FB}$
En effet, $\overrightarrow{FB}= \overrightarrow{EA}$. Or la droite $(AE)$ appartient au plan $(DEH)$. Ainsi $\overrightarrow{FB}$ est coplanaire à $\overrightarrow{DH}$ et $\overrightarrow{ED}$ : $\overrightarrow{FB}$ est donc une combinaison linéaire des deux précédents.
On regardera si les vecteurs appartiennent à un même plan

En effet, $3 \overrightarrow{AC} + 5 \overrightarrow{AD} = \left ( \begin{array}{c} 3\times 2 + 5\times(-1) \\ 3\times (-1) + 5\times 1 \\ 3\times (-1)\end{array} \right ) = \overrightarrow{AB}$