Fiche de cours
Combinaisons linéaires de vecteurs de l'espace
Propriété :
Soient $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ trois vecteurs de l'espace non nuls,
On dit que $\overrightarrow{w}$ est une combinaison linéaire de $\overrightarrow{u}$ et de $\overrightarrow{v}$ s'il existe $\alpha, \beta \in \mathbb{R}$ tel que
$\overrightarrow{w}=\alpha \overrightarrow{u}+ \beta \overrightarrow{v}$
$\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ sont alors coplanaires, c'est à dire qu'ils appartiennent à un même plan.
Exercice 1
Soit $ABCDEFGH$ un pavé droit et $I$ cette de $ABCD$,
On pose $\overrightarrow{u} = 3\overrightarrow{AB}$, $\overrightarrow{v} = \overrightarrow{BD} + \overrightarrow{BE}$ et $\overrightarrow{w} = 3\overrightarrow{AI} + \overrightarrow{IE}$
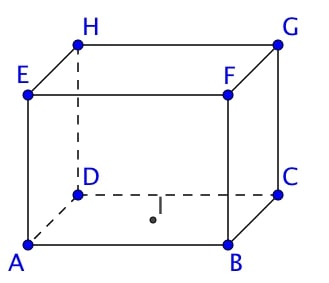
Montrer que $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ sont coplanaires.
$\begin{aligned} \overrightarrow{u} &= 3 \overrightarrow{AB} \\ &= 3 \overrightarrow{AI} + 3\overrightarrow{IB} \\ &= 3 \overrightarrow{AI} + \overrightarrow{IB} + 2\overrightarrow{IB} \\ &= 3 \overrightarrow{AI} + \overrightarrow{IE} + \o
