L'énoncé
Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Rappeler la définition d'une base de l'espace.
$\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ constituent une base de l'espace si et seulement si il n'existe pas de combinaisons linéaires de $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$.
$\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ constituent une base de l'espace si et seulement si il existe au moins une combinaison linéaire de $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$.
$\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ constituent une base de l'espace si et seulement si $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ ne sont pas colinéaires.
On pourra revoir la vidéo du cours au besoin
Question 2
Soit $ABCDEFGH$ un cube et $M$ le milieu de $[EF]$,
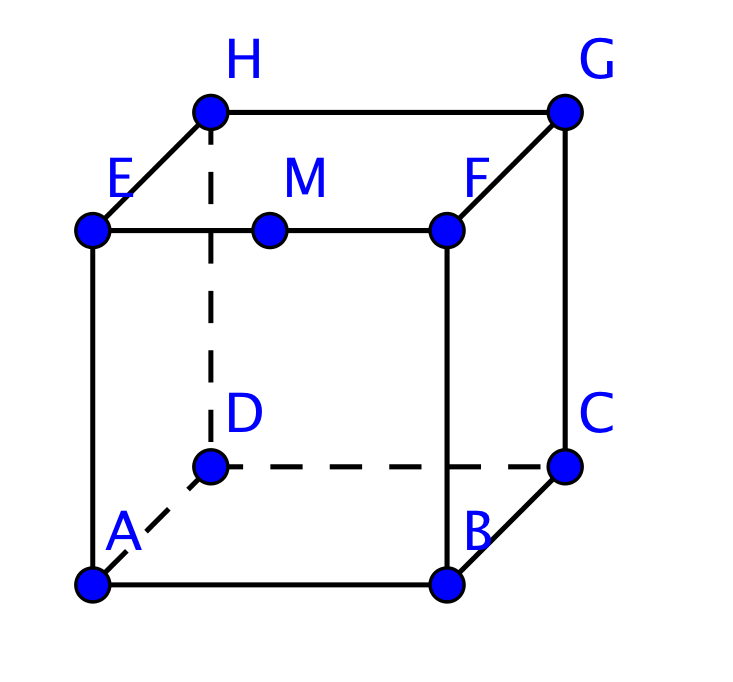
Quels triplets forment une base de l'espace ?
$(\vec{AB}, \vec{AD}, \vec{AE})$
En effet, $\vec{AE}$ est normal au plan $ABD$. Les vecteurs ne sont donc pas coplanaires : ils forment donc une base de l'espace.
$(\vec{AB}, \vec{AE}, \vec{DG})$
En effet $\vec{AB}+\vec{AE} = \vec{DG}$.
Ainsi il existe au moins une combinaison linéaire des trois vecteurs.
Ils ne forment donc pas une base.
$(\vec{BC}, \vec{DH}, \vec{EF})$
En effet, $\vec{BC} = \vec{FG}$. En outre, $\vec{DH}$ est normal au plan $EFG$. Les vecteurs ne sont donc pas coplanaires : ils forment donc une base de l'espace.
On pourra se demander si les vecteurs appartiennent au même plan.
Question 3
Soit $ABCDEFGH$ un cube et $M$ le milieu de $[EF]$,

Quels triplets ne forment pas une base de l'espace ?
($\vec{HG}$, $\vec{HE}$, $\vec{HD}$)
($\vec{HD}$, $\vec{AM}$, $\vec{EF}$)
En effet, $\vec{AM} = -\vec{HD} + \dfrac{1}{2} \vec{EF}$.
Ainsi, les coefficients multiplicateurs ne sont pas nuls.
Donc ($\vec{HD}$, $\vec{AM}$, $\vec{EF}$) ne forment pas une base.
($\vec{BC}$, $\vec{AE}$, $\vec{HG}$)
On pourra chercher une combinaison linéaire de vecteurs dont les coefficients sont non nuls.
Question 4
Soient $\overrightarrow{u}(-2; 2; 1)$, $\overrightarrow{v}(1; -1; 3)$ et $\overrightarrow{w}(0; -1; 2)$.
Quelle est la bonne combinaison linéaire ?
$\overrightarrow{u} + 2 \overrightarrow{v} + \overrightarrow{w} = \overrightarrow{0}$
$\overrightarrow{u} - \overrightarrow{v} + \overrightarrow{w} = \overrightarrow{0}$
Il n'existe pas de combinaison linéaire non nulle.
En effet, soient $(\alpha, \beta, \gamma) \in \mathbb{R}^3$,
$\alpha\overrightarrow{u} + \beta\overrightarrow{v} + \gamma\overrightarrow{w} = \overrightarrow{0}$
$\iff \left \{ \begin{array}{lcc} -2\alpha + \beta &=& 0 \\ 2 \alpha - \beta - \gamma &=& 0 \\ \alpha + 3 \beta + 2\gamma &=& 0 \end{array} \right.$
$\iff \left \{ \begin{array}{lcc} \beta &=& 2\alpha \\ 2 \alpha - 2 \alpha - \gamma &=& 0 \\ \alpha + 6 \alpha + 2\gamma &=& 0 \end{array} \right.$
$\iff \left \{ \begin{array}{lcc} \beta &=& 2\alpha \\ \gamma &=& 0 \\ 7 \alpha &=& 0 \end{array} \right.$
$\iff \left \{ \begin{array}{lcc} \beta &=& 0 \\ \gamma &=& 0 \\ \alpha &=& 0 \end{array} \right.$
Essayer d'écrire un système faisant intervenir $(\alpha, \beta, \gamma)$
Question 5
Soient $\overrightarrow{u}(-2; 2; 1)$, $\overrightarrow{v}(1; -1; -0,5)$ et $\overrightarrow{w}(0; -1; 2)$.
Quelle est la bonne combinaison linéaire ?
$\overrightarrow{u} + 2\overrightarrow{v} = \overrightarrow{0}$
En effet, soient $(\alpha, \beta, \gamma) \in \mathbb{R}^3$,
$\alpha\vec{u} + \beta\vec{v} + \gamma\vec{w} = \vec{0}$
$\iff \left \{ \begin{array}{lcc} -2\alpha + \beta &=& 0 \\ 2 \alpha - \beta - \gamma &=& 0 \\ \alpha - 0.5 \beta + 2\gamma &=& 0 \end{array} \right.$
$\iff \left \{ \begin{array}{lcc} \beta &=& 2\alpha \\ 2 \alpha - 2 \alpha - \gamma &=& 0 \\ \alpha - \alpha + 2\gamma &=& 0 \end{array} \right.$
$\iff \left \{ \begin{array}{lcc} \beta &=& 2\alpha \\ \gamma &=& 0 \\ 0 &=& 0 \end{array} \right.$
$\iff \beta = 2\alpha$
Ainsi, si $\alpha = 1$ alors $\beta = 2$
$2\overrightarrow{u} + 4\overrightarrow{v} = \overrightarrow{0}$
En effet, soient $(\alpha, \beta, \gamma) \in \mathbb{R}^3$,
$\alpha\overrightarrow{u} + \beta\overrightarrow{v} + \gamma\overrightarrow{w} = \overrightarrow{0}$
$\iff \left \{ \begin{array}{lcc} -2\alpha + \beta &=& 0 \\ 2 \alpha - \beta - \gamma &=& 0 \\ \alpha - 0.5 \beta + 2\gamma &=& 0 \end{array} \right.$
$\iff \left \{ \begin{array}{lcc} \beta &=& 2\alpha \\ 2 \alpha - 2 \alpha - \gamma &=& 0 \\ \alpha - \alpha + 2\gamma &=& 0 \end{array} \right.$
$\iff \left \{ \begin{array}{lcc} \beta &=& 2\alpha \\ \gamma &=& 0 \\ 0 &=& 0 \end{array} \right.$
$\iff \beta = 2\alpha$
Ainsi, si $\alpha = 2$ alors $\beta = 4$
Il n'existe pas de combinaison linéaire non nulle.
Essayer d'écrire un système faisant intervenir $(\alpha, \beta, \gamma)$

C'est la bonne définition.