Fiche de cours
Suites convergentes
Définition :
Une suite de réels $(u_n)_{(n \in \mathbb{N})}$ converge vers le réel $l$ si et seulement tout intervalle ouvert contenant $l$ contient tous les termes de la suite à partir d'un certain rang.
On note alors $\lim \limits _{n \to + \infty} u_n = l$.
Ce formalise, introduit par Karl Weierstrass au 19e siècle, est nécessaire pour appréhender correctement les infiniment petit ou grand, pour lesquels l'intuition ne suffit pas.
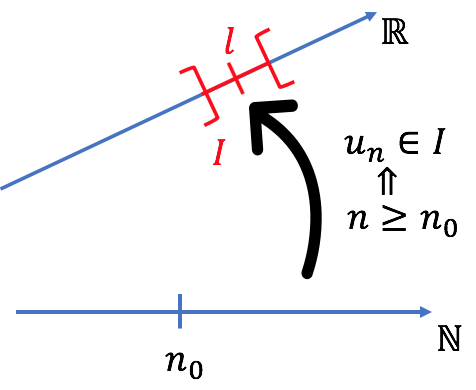
On trace la droite des réels et la "droite" des entiers naturels. Soit un réel $l$ fixé, pour tout intervalle $I$ ouvert contenant $l$, il existe un rang $n_0$ à partir duquel tous les termes de la suite appartiennent à $I$.
$I$ peut être choisi aussi petit que possible, non vidé ouvert autour de $l$. Cela signifie que la quasi totalité des termes de la suite appartient à $I$. En effet, seuls les termes de $0$ à $n_0 -1$ n'appartiennent pas à $I$ : il y en a donc un nombre fini. Intuitivement, en se rapprochant du nombre $l$, la "densité" de termes $u_n$ augmente.
Math&eacu
