On considère la fonction $f$ définie sur l’ensemble  des nombres réels $\mathbb{R}$  par :

$f(x)= (ax + b)e^{x-1}+c $, où $a, b$ et $c$ sont trois réels que l’on se propose de déterminer dans la partie A.

On note $f’$ la fonction dérivée de $f$.

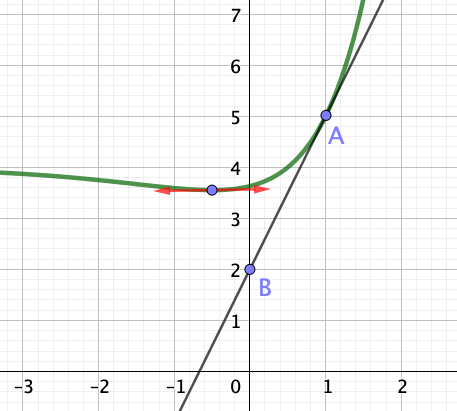
La courbe $C$ représentative de $f$ dans le plan rapporté à un repère orthonormal est représentée ci-dessous.

La courbe $C$ passe par le point $A(1 ; 5)$, elle admet la droite $\Delta$ comme tangente en ce point.

Le point $B(0 ; 2)$ appartient à la droite $\Delta$.

La courbe $C$ admet également une tangente horizontale au point d’abscisse $-\dfrac{1}{2}$

PARTIE A 

1) a) Préciser les valeurs de $f(1)$ et $f’(-\dfrac{1}{2})$

    b) Déterminer le coefficient directeur de la droite $\Delta$. En déduire $f’(1)$.

2) Montrer que, pour tout réel $x$, $f’(x) = (ax+ a + b)e^{x-1}$.

3) Montrer que $a, b$ et $c$ vérifient le système : $\begin{cases}  a+b+c=5 \\ a+2b=0  \\ 2a+b=3 \end{cases}$. Déterminer les valeurs de $a, b$ et $c$.

PARTIE B

On admet pour la suite de l’exercice que, pour tout réel $x$, $f(x) = (2x – 1) e^{x-1}+ 4$.

1) a) Déterminer $\displaystyle\lim_{x \to +\infty}f(x)$.

     b) Vérifier que, pour tout réel x, $f(x) = \dfrac{2}{e}xe^x–\dfrac{1}{e}e^x+ 4$. En déduire $\displaystyle\lim_{x \to -\infty}f(x)$. (on rappelle que $\displaystyle\lim_{x \to -\infty} xe^x $=0). Que peut-on en déduire pour la courbe $C$ ?

2) a) Donner, pour tout réel $x$, l’expression de $f’(x)$.

     b) Établir le tableau de variation de $f$. Déterminer le signe de $f(x)$ pour tout réel $x$.

     c) Montrer que l’équation $f(x) = 6$ admet une unique solution réelle $a$ sur l’intervalle $[1 ;2]$. On donnera un encadrement de $a$ d’amplitude 0,1.

PARTIE C

1) On considère la fonction $F$ définie pour tout réel x par $F(x) = (2x−3) e^{x-1} + 4x$. Montrer que $F$ est une primitive de $f$ sur $\mathbb{R}$.

2) Soit $D$ la partie du plan située entre la courbe $C$, l’axe des abscisses et les droites d’équations $x = 0$ et $x = 1$. 

Calculer l’aire de la partie $D$ exprimée en unités d’aire ; on donnera la valeur exacte et la valeur décimale arrondie au dixième.