L'énoncé
Soit \(f\) la fonction \(f\) définie sur l'intervalle \(\left[0;\dfrac{\pi}{2}\right]\) par \(f(x) = (1+\sin(x)) \times \cos(x)\)
Cet exercice commence par l'étude de la fonction \(f\) sur l'intervalle \(\left[0;\dfrac{\pi}{2}\right]\), puis s'intéresse ensuite à la représentation graphique de \(f\) sur \(\left[0;\dfrac{\pi}{2}\right]\).
Question 1
Justifier que \(f\) est dérivable sur \(\left[0;\dfrac{\pi}{2}\right]\) et montrer que \(f ' (x) = -2\sin^2(x) -\sin(x) +1\)
\(f\) est le produit de deux fonctions dérivables sur\(\left[0;\dfrac{\pi}{2}\right]\) donc \(f\) est dérivable sur\(\left[0;\dfrac{\pi}{2}\right]\).
On pose : \(u(x) = 1+\sin(x)\) et \(v(x) = \cos(x)\)
On a : \(u'(x) = \cos(x)\) et \(v'(x) = -\sin(x)\)
Donc : \(f'(x) = (\cos(x)) \times \cos(x)+(1+\sin(x)) \times (-\sin(x)))\)
\(f'(x)= \cos^2(x)-\sin(x)-\sin^2(x)\)
\(f'(x)= 1-\sin^2(x)-\sin(x)-\sin^2(x)\)
\(f'(x)= -2\sin^2(x) - \sin(x)+1\)
Avez-vous repéré la formule de dérivation à appliquer ici ?
On utilise \((u \times v)' = u'v+uv'\).
On pose : \(\begin{array}{lcl} u(x) = 1+sinx \\ v(x) = cosx \end{array}\)
Une fois qu'on a la dérivé, il faut l'exprimer uniquement en fonction de \(sinx\) pour arriver à l'écriture proposée dans la question : il faut donc ne plus avoir le \(cos^2x\) : penser aux formules de trigonométrie où figure \(cos^2x\)...
C'est \(\cos^2(x)+\sin^2(x)=1\) qu'il faut appliquer !
Question 2
Factoriser le polynôme \(-2X^2-X+1\).
On cherche d'abord les racines de \(-2X^2-X+1\) :
Le discriminant est : \(\Delta = 1-4 \times (-2) = 9\)
Les solutions de \(-2X^2-X+1 = 0\) sont donc :
\(X_1 = \dfrac{1+3}{-4} = -1\) et \(X_2 = \dfrac{1-3}{-4}= \dfrac{1}{2}\)
D'où la factorisation : \(-2X^2-X+1 = -2(X+1)\left(X-\dfrac{1}{2}\right)\)
Quelles formules faut-il utiliser ici ? Il y a du second degré…
Pour factoriser un polynôme du second degré, on calcule les racines, puis on utilise l’égalité : \(ax^2 + bx + c = a(x - x_1)(x - x_2)\)
Question 3
En déduire la forme factorisée de \(f'(x)\).
On a : \(f'(x) = -2\sin^2(x)-\sin(x)+1\)
En posant \(X=\sin(x)\), on peut exploiter l'égalité obtenue dans la question 2 : \(-2X^2-X+1=-2(X+1)\left(X-\dfrac{1}{2}\right)\)
Donc :
\(-2\sin^2(x)-\sin(x)+1 = -2(\sin(x)+1)(\sin(x)-\frac{1}{2})\) En conclusion : on a donc la forme factorisée de la dérivée :
\(f'(x) = -2(\sin(x)+1)(\sin(x)-\frac{1}{2})\)
Grâce à cette écriture, nous allons étudier le signe de la dérivée.
Vois-tu le lien entre la dérivée de \(f\) et la question 2a) ? Un indice : on met \(\sin(x)\) à la place de \(X\).
On remplace donc \(X\) par \(\sin(x)\) dans l'égalité \(-2X^2-X+1=-2(X+1)\left(X-\dfrac{1}{2}\right)\)
Question 4
En déduire le tableau de signe de \(f (x)\) sur \(\left[0;\dfrac{\pi}{2}\right]\)
Le signe de \(f'(x)\) dépend du signe de \(\sin(x)+1\) et du signe de \(\sin(x)-\dfrac{1}{2}\) :
- Pour le signe de \(\sin(x)-\dfrac{1}{2}\) :
On va résoudre par exemple l'inéquation \(\sin(x)-\dfrac{1}{2} \leq 0\) pour ensuite établir le tableau de signe de cette écriture :
\(\sin(x)-\dfrac{1}{2} \leq 0 \Leftrightarrow \sin(x) \leq \dfrac{1}{2}\)
On sait déjà que \(\sin(\frac{\pi}{6}) = \dfrac{1}{2}\), et par lecture sur le cercle trigonométrique, on voit que :
\(\sin(x) \leq \dfrac{1}{2} \Leftrightarrow x \in \left[0;\dfrac{\pi}{6}\right]\)
N'oublions pas lors de cette lecture que l'on étudie la fonction \(f\) uniquement sur l'intervalle \(\left[0;\dfrac{\pi}{2}\right]\), ce qui fait que la lecture du cercle ne se fait pas que sur le premier "quadrant").
- Pour le signe de \(\sin(x)+1\) :
On sait que \(-1 \leq \sin(x) \leq 1\) donc on a :
\(0 \leq \sin(x)+1 \leq 2\). On a donc :
\(\sin(x)+1\) est positif sur \(\left[0; \frac{\pi}{2}\right]\).
En conclusion, on peut construire le tableau de signe de \(f'(x)\) :
Comme toujours dans une étude signe, on utilise la forme factorisée de la dérivée : l’avez-vous ici ?
Pour établir le tableau de signes, on a besoin de connaître le signe de \(\sin(x) +1\) et de \(\sin(x) - \dfrac{1}{2}\)
Essaye de résoudre (séparément) les inéquations : \(\sin(x) + 1 \leq 0\) et \(\sin(x) - \dfrac{1}{2} \leq 0\).
Et pense que l'étude est juste menée sur l'intervalle \(\left[0;\dfrac{\pi}{2}\right]\).
En vrac, voici quelques outils pour t'aider : on sait que \(-1 \leq \sin(x) \leq 1\) et \(\sin\frac{\pi}{6} = \dfrac{1}{2}\).
Et bien sûr, n’oublie pas les lectures sur le cercle trigonométrique pour résoudre une inéquation trigonométrique : vas voir la vidéo !
Une fois que tu as les solutions de \(\sin(x) + 1 \leq 0\) et \(\sin(x) - \dfrac{1}{2} \leq 0\), tu peux construire le tableau de signe de \(f&rsqu
Question 5
En déduire le tableau de variations de \(f\) sur \(\left[0;\dfrac{\pi}{2}\right]\).
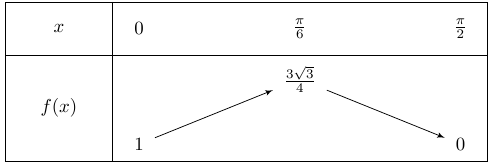
En effet :
\(f\left(\dfrac{\pi}{6}\right) = \left( 1+\sin(\frac{\pi}{6})\right) \times \cos(\frac{\pi}{6})\)
\(f\left(\dfrac{\pi}{6}\right) = \left(1+\dfrac{1}{2} \right) \times \dfrac{\sqrt{3}}{2} \)
\(f\left(\dfrac{\pi}{6}\right) = \dfrac{3\sqrt{3}}{4}\)
\(f(0) = (1+\sin(0)) \times \cos(0) =1\)
\(f\left(\dfrac{\pi}{2}\right) = \left(1+\sin(\frac{\pi}{2})\right) \times \cos(\frac{\pi}{2}) =0\)
Il ne devrait pas y avoir de problème pour les flèches et le sens de variations… Mais pensez à compléter le tableau par les images, il y en a 3 à calculer ici…
Question 6
On se place maintenant sur l'intervalle \([0 ; \pi]\).
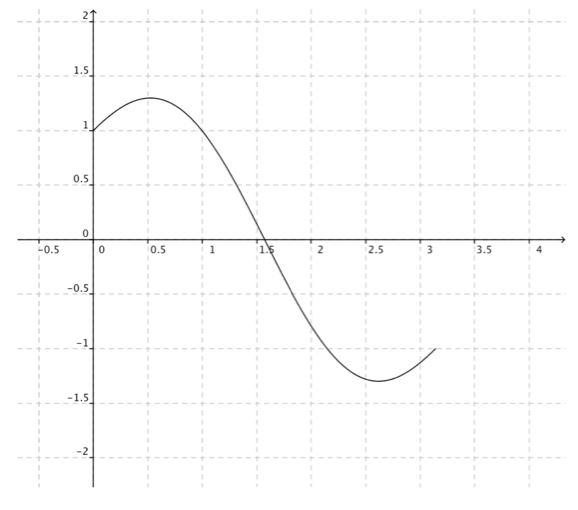
On souhaite construire la courbe représentative de \(f\) sur cet intervalle.
Vérifier que pour tout réel \(h\), on a :
\(f \left( \dfrac{\pi}{2}-h\right) = -f \left( \dfrac{\pi}{2}+h\right)\)
On a (grâce aux formules sur les angles associés) :
\(f \left( \dfrac{\pi}{2}-h\right)= \left(1+\sin \left(\frac{\pi}{2}-h\right) \right) \times \cos \left( \frac{\pi}{2}-h\right)\)
\(f \left( \dfrac{\pi}{2}-h\right)= (1+\cos(h)) \times \sin(h)\)
En effet, on voit grâce au cercle trigonométrique que l'on a les égalités suivantes :
\(\sin\left( \frac{\pi}{2}-h\right) = \cos(h)\)
\(\cos\left( \frac{\pi}{2}-h\right)= \sin(h)\)
De même, on fait le calcul, en utilisant cette fois que:
\(\sin\left( \frac{\pi}{2}+h\right) = \cos(h)\) et \(\cos\left(\frac{\pi}{2}+h\right) = -\sin(h)\)
\(f \left( \dfrac{\pi}{2}+h\right)= \left(1+\sin \left(\frac{\pi}{2}+h\right) \right) \times \cos \left( \frac{\pi}{2}+h\right)\)
\(f \left( \dfrac{\pi}{2}+h\right)= (1+\cos(h)) \times (-\sin(h)) \)
\(f \left( \dfrac{\pi}{2}+h\right)= -(1+ \cos(h))\times \sin(h)\)
En conclusion, on a bien \(f \left( \dfrac{\pi}{2}+h\right) = -f \left( \dfrac{\pi}{2}-h\right)\)
Sur le plan de la méthode, il faut déjà former les écritures \(f \left( \frac{\pi}{2}-h\right)\) et \(f \left( \frac{\pi}{2}+h\right)\) et ensuite essayer d’obtenir des écritures plus simples grâce aux formules trigonométriques.
On a que \(\sin\left( \frac{\pi}{2}+h\right) = \cos(h)\) et \(\cos \left( \frac{\pi}{2}+h\right)= -\sin(h)\).
Et aussi \(\sin\left( \frac{\pi}{2}-h\right) = \cos(h)\) et \(\cos \left( \frac{\pi}{2}-h\right)= \sin(h)\)
Avec tout ça, vous pouvez démontrer l’égalité demandée.
Question 7
Que peut-on en déduire pour la courbe représentative de \(f\) ?
L'égalité obtenue précédemment montre que le point \(I\) de coordonnées \( \left(\frac{\pi}{2} ; 0\right)\) est centre de symétrie de la courbe.
En effet, si lon prend deux points \(M\) et \(M'\) ayant pour abscisses respectives \( \left(\frac{\pi}{2} -h \right)\) et \( \left(\frac{\pi}{2} +h \right)\),
alors les coordonnées de ces deux points sont : \( f\left(\frac{\pi}{2} -h \right)\) et \(f \left(\frac{\pi}{2} +h \right)\).
Le point \(I\) est alors le milieu du segment \([MM']\) car :
\( \left\{ \begin{array}{ll} \dfrac{x_M + x_{M'}}{2} = \dfrac{\frac{\pi}{2}-h +\frac{\pi}{2} +h}{2} \\ \dfrac{y_M + y_{M'}}{2} = \dfrac{f \left( \frac{\pi}{2}-h \right) + f \left( \frac {\pi}{2} +h \right)}{2} \end{array} \right.\)
\( \left\{ \begin{array}{ll} \dfrac{x_M + x_{M'}}{2} = \dfrac{\pi}{2} = x_I \\ \dfrac{y_M + y_{M'}}{2} = \dfrac{f \left( \frac{\pi}{2}-h \right) - f \left( \frac {\pi}{2} -h \right)}{2} = 0 = y_I \end{array} \right.\)
Aidez-vous d’une figure : faites un repère, placez à peu près \(\dfrac{\pi}{2}\) sur l’axe des abscisses, puis son image \(f (\dfrac{\pi}{2}) = 0\), et ensuite placez les abscisses \(\dfrac{\pi}{2}-h\) et \(\dfrac{\pi}{2}+h\) : elles sont situées de part et d’autre de \(\dfrac{\pi}{2}\).
Essayez maintenant de voir ce qui se passe si leurs images sont opposées, car n’oublions pas que l’on a : \(f \left( \dfrac{\pi}{2}-h\right) = -f \left( \dfrac{\pi}{2}+h\right)\).
On peut normalement dégager une propriété de symétrie sur les points ainsi obtenus : l'avez-vous repérée ?
Tout se joue par rapport au point \(I\) de coordonnées \( \left(\frac{\pi}{2} ; 0\right)\) : si l’on note \(M\) et \(M’\) les points de coordonnées respectives :
\(M = \left(\dfrac{\pi}{2}-h ; f\left(\dfrac{\pi}{2}-h\right)\right)\)
\(M' = \left(\dfrac{\pi}{2}+h ; f\le
Question 8
Déterminer l'équation de la tangente à \(C_f\) au point d'abscisse \(\dfrac{\pi}{2}\).
On sait que l'équation cherchée est \(y = f '(a)(x -a)+ f(a)\) avec \(a=\dfrac{\pi}{2}\)
Ici, \(y = f '\left(\dfrac{\pi}{2}\right)\left(x -\dfrac{\pi}{2}\right)+ f\left(\dfrac{\pi}{2}\right)\)
Avec :
\(f \left(\dfrac{\pi}{2}\right)= 0\) et
\(f' \left(\dfrac{\pi}{2}\right) = -2 \sin^2 \left(\frac{\pi}{2}\right)- \sin( \frac{\pi}{2}) +1 = -2-1+1 = -2\)
Soit pour l'équation demandée :
\(y = -2 \left( x- \dfrac{\pi}{2}\right) + 0\)
\(y = -2x + \pi\)
Un grand classique évidemment : l’équation d’une tangente ! Formule à connaître par cœur, et sans erreur dans les signes.... Voir la deuxième astuce en cas de doute !
La tangente au point d’abscisse a est donnée par : \(y = f '(a)(x -a)+ f(a)\). Quelle est la valeur de \(a\) ici ?
On a besoin de \(f \left(\frac{\pi}{2}\right)\) et \(f' \left(\frac{\pi}{2}\right)\) : vous avez toutes les formules à votre disposition, il suffit de remplacer !
Question 9
Tracer la courbe de \(f\) sur l'intervalle \([0; \pi]\).
On trace ensuite la courbe de \(f\) sur l'intervalle \(\left[0; \dfrac{\pi}{2}\right]\), puis ensuite on complète en utilisant le centre de symétrie \(I\).
Prennez plusieurs points pour bien tracer la courbe : la construction est souvent bien notée !