On considère la fonction suivante. $f(x)= \dfrac{-x+1}{x+3}$ sur $D= \mathbb{R}- \{-3\} $
1) Calculer les limites aux bornes de son ensemble de définition $D$ et déterminer une équation de chacune des éventuelles asymptotes horizontales et/ou verticales
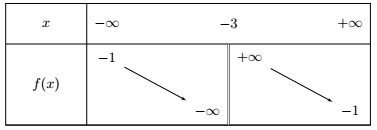
2) Calculer sa dérivée et en déduire ses variations.
3) A l'aide de la calculatrice, représentez la fonction dans un repère.
1) La fonction $f$ est définie sur $D=]-\infty;-3[ \cup ]-3;+\infty[$ par : $f(x)= \dfrac{-x+1}{x+3}$.
On a : $\begin{cases} \displaystyle\lim_{x \to -\infty} -x+1= +\infty \\ \displaystyle\lim_{x \to -\infty} x+3 = -\infty \end{cases}$.
Les règles de calcul sur les limites ne permettent pas de conclure directement.
Cependant, pour $x \in D$ et $x$ non nul, on peut écrire :
$ f(x)= \dfrac{x\bigg(-1+ \dfrac{1}{x}\bigg)}{x\bigg(1+ \dfrac{3}{x}\bigg)}= \dfrac{-1+ \dfrac{1}{x}}{1+ \dfrac{3}{x}}$
On en déduit : $\displaystyle\lim_{x \to -\infty} f(x)=-1$.
De la même façon, on démontre que : $\displaystyle\lim_{x \to +\infty} f(x)=-1$.
La courbe d'équation $y=f(x)$ admet donc une asymptote horizontale d'équation $y=-1$.
Étudions les limites de $f$ en -3.
On a : $\begin{cases} \displaystyle\lim_{x \to -3} -x+1= 4 \\ \displaystyle\lim_{x \to -3} x+3 = 0 \end{cases}$
En passant au quotient la limite en -3 de $f$ est infinie.
Plus précisément, si $x<-3$ alors $x+3<0$ donc :
$ \displaystyle\lim_{\substack{x \to -3 \\ x<-3}} f(x)=-\infty$
Et si $x>-3$ alors $x+3>0$ donc :
$ \displaystyle\lim_{\substack{x \to -3 \\ x>-3}} f(x)=+\infty$
La courbe représentant la fonction $f$ admet donc une asymptote verticale d'équation $x=-3$.
2) $f$ est dérivable sur son ensemble de définition. Calculons la dérivée de $f$ :
Posons $\begin{cases} u(x)=-x+1 \\ v(x)=x+3 \end{cases}$, on en déduit : $\begin{cases} u'(x)=-1 \\ v'(x)=1 \end{cases}$.
On sait que $\bigg( \dfrac{u}{v} \bigg)'= \dfrac{u'v-uv'}{v^2}$.
Donc, $\fbox{$f'(x)=\dfrac{-(x+3)-(-x+1)}{(x+3)^2}=-\dfrac{4}{(x+3)^2}$}$.
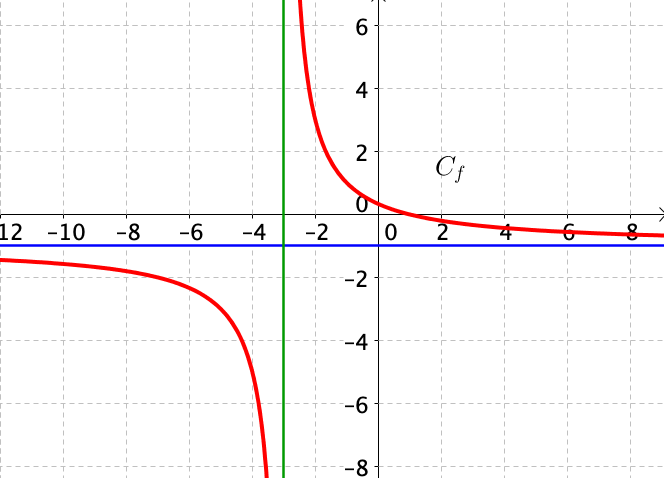
3) Voici la représentation graphique :