L'énoncé
\(f\) est la fonction définie par \(f(x)=\dfrac{2x^2+x-1}{x^2+x}\) sur \(D=\left[-\dfrac{1}{2};0 \right[\cup\left]0;+\infty\right[\).
On note \(C_f\) sa courbe représentative dans un repère \((O,\vec{i},\vec{j})\).
Question 1
Déterminer les coordonnées du point d'intersection de \(C_f\) avec l'axe des abscisses.
Intersection avec les axes des abscisses :
Il faut résoudre \(f(x)=0\) sur \(D=\left[-\frac{1}{2};0\right[\cup]0;+\infty[\)
$x^2+x$ s'annule en $-1$ et en $0$ donc comme ces deux nombres sont hors du domaine d'étude,
\(\dfrac{2x^2+x-1}{x^2+x}=0 \Leftrightarrow 2x^2+x-1=0\)
On calcule le discriminant : \(\Delta = b^2-4ac=1^2-4\times 2\times (-1)=9\)
L'équation \(2x^2+x-1=0\) possède donc deux solutions :
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-1+3}{4}=\dfrac{1}{2}\)
et \(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-1-3}{4}=-1\)
Mais comme l'étude se fait sur \(D=\left[-\frac{1}{2};0\right[\cup]0;+\infty[\), on ne garde que la solution \(x_1=\dfrac{1}{2}\).
Conclusion : La courbe ne coupe qu'une seule fois l'axe des abscisses au point de coordonnées \(\left(\dfrac{1}{2};0\right)\)
Il faut résoudre \(f(x)=0\).
\(f(x)=0\) équivaut à \(2x^2+x-1\) =?
C’est un type d’équation familière…
Calculez le discriminant !
Question 2
Etudier la limite de \(f\) en $0$, puis en \(+\infty\).
Préciser alors les asymptotes éventuelles de \(C_f\).
Limite en O :
Méthode 1 :
On sait qu'en $0$, une fraction rationnelle a même limite que le quotient des termes de plus bas degré (ici c'est \(-\dfrac{1}{x}\) : il faut distinguer limite à gauche et à droite de $0$).
On a donc :
\(\displaystyle\lim_{\substack{x \to 0 \\ x>0}}f(x)=\displaystyle\lim_{\substack{x \to 0 \\ x>0}}\dfrac{2x^2+x-1}{x^2+x}=\displaystyle\lim_{\substack{x \to 0 \\ x>0}}-\dfrac{1}{x}=-\infty\)
\(\displaystyle\lim_{\substack{x \to 0 \\ x<0}}f(x)=\displaystyle\lim_{\substack{x \to 0 \\ x<0}}\dfrac{2x^2+x-1}{x^2+x}=\displaystyle\lim_{\substack{x \to 0 \\ x<0}}-\dfrac{1}{x}=+\infty\)
Méthode 2 : on détaille tout ! (à regarder pour fixer les choses, mais la méthode 1 est plus rapide
)
\(\displaystyle\lim_{\substack{x \to 0}}2x^2+x-1=-1\)
\(\displaystyle\lim_{\substack{x \to 0}}x^2+x=0\)
Donc on obtient une limite du type "\(-\dfrac{1}{0}\)".
Il faut savoir si \(x^2+x\) tend vers 0 en étant positif ou négatif. On a donc besoin du signe de cette écriture.
On a : \(x^2+x=x(x+1)\)
On a en particulier que :
- Pour \(-1<x<0\), \(x(x+1)<0\)
- Pour \(x>0\), \(x(x+1)>0\)
On écrit alors les limites à droite et à gauche de $0$ :
\(\displaystyle\lim_{\substack{x \to 0 \\ x<0}}x(x+1)=0\) en étant négatif donc :
\(\displaystyle\lim_{\substack{x \to 0 \\ x<0}}\dfrac{1}{x(x+1)}=-\infty\)
Alors :
\(\left. \begin{array}{rcl} \displaystyle \displaystyle\lim_{\substack{x \to 0 \\ x<0}}\dfrac{1}{x(x+1)} & = & -\infty\\ \\ \displaystyle\lim_{\substack{x \to 0}}2x^2+x-1 & = & -1\\ \end{array} \right\}\) \(\displaystyle\lim_{\substack{x \to 0 \\ x<0}}\dfrac{2x^2+x-1}{x^2+x}=\displaystyle\lim_{\substack{x \to 0 \\ x<0}}(2x^2+x-1)\times \dfrac{1}{x^2+x}=+\infty\)
\(\displaystyle\lim_{\substack{x \to 0 \\ x>0}}x(x+1)=0\) en étant positif donc \(\displaystyle\lim_{\substack{x \to 0 \\ x>0}}\dfrac{1}{x(x+1)}=+\infty\) Alors :
\(\left. \begin{array}{rcl} \displaystyle \displaystyle\lim_{\substack{x \to 0 \\ x>0}}\dfrac{1}{x(x+1)} & = & +\infty\\ \\ \displaystyle\lim_{\substack{x \to 0}}2x^2+x-1 & = & -1\\ \end{array} \right\}\) \(\displaystyle\lim_{\substack{x \to 0 \\ x>0}}\dfrac{2x^2+x-1}{x^2+x}=\displaystyle\lim_{\substack{x \to 0 \\ x>0}}(2x^2+x-1)\times \dfrac{1}{x^2+x}=-\infty\)
Conclusion :
On a démontré que : \(\displaystyle\lim_{\substack{x \to 0 \\ x<0}}f(x)=+\infty \) et \(\displaystyle\lim_{\substack{x \to 0 \\ x>0}}f(x)=-\infty \).
Conséquence graphique : la droite d'équation \(x=0\) est asymptote verticale (c'est l'axe des ordonnées).
Limite en \(+\infty\) :
\(f\) est une fraction rationnelle : d'après le cours, la limite de \(f\) en l'infini est donc égale à la limite du quotient des termes de plus haut degré (ici, c'est \(2x^2\) pour le numérateur et \(x^2\) pour le dénominateur).
On a donc : \(\displaystyle\lim_{\substack{x \to +\infty}}f(x)=\displaystyle\lim_{\substack{x \to +\infty}}\dfrac{2x^2}{x^2}=\displaystyle\lim_{\substack{x \to +\infty}}2=2\)
Conséquence graphique : la droite d'équation \(y=2\) est asymptote horizontale à \(C_f\) en \(+\infty\).
Il faut distinguer deux cas : on a besoin de calculer \(\lim\limits_{\substack{x \to 0 \\ x<0}}f(x)\) et \(\lim\limits_{\substack{x \to 0 \\ x>0}}f(x)\).
Voir la vidéo de rappel sur les opérations sur les limites.
Au voisinage de l’infini, on a aussi une règle pour les fractions rationnelles…
Regarder le quotient des termes de plus haut degré !
Question 3
Justifier que \(f\) est dérivable sur \(D\), puis déterminer la dérivée de \(f\).
3) a. \(f\) est dérivable sur \(D\) car c'est une fraction rationnelle (quotient de deux polynômes), bien définie sur \(D\).
Calcul de la dérivée de \(f\) :
\(u(x)=2x^2+x-1\) alors \(u'(x)=4x+1\)
\(v(x)=x^2+x\) alors \(v'(x)=2x+1\)
\(f'(x)=\dfrac{u'(x).v(x)-u(x).v'(x)}{v(x)^2}\)
\(f'(x)=\dfrac{(4x+1).(x^2+x)-(2x^2+x-1).(2x+1)}{(x^2+x)^2}\)
\(f'(x)=\dfrac{4x^3+4x^2+x^2+x-(4x^3+2x^2+2x^2+x-2x-1)}{(x^2+x)^2}\)
\(f'(x)=\dfrac{4x^3+5x^2+x-(4x^3+4x^2-x-1)}{(x^2+x)^2}\)
\(f'(x)=\dfrac{4x^3+5x^2+x-4x^3-4x^2+x+1}{(x^2+x)^2}\)
\(f'(x)=\dfrac{x^2+2x+1}{(x^2+x)^2}\)
\(f'(x)=\dfrac{(x+1)^2}{(x^2+x)^2}\)
On peut s'arrêter là dans le calcul ou remarquer que ce quotient est simplifiable par \(x+1\) :
On obtient alors :
\(f'(x)=\dfrac{(x+1)^2}{\left(x(x+1)\right)^2}=\left(\dfrac{x+1}{x(x+1)}\right)^2=\left(\dfrac{1}{x}\right)^2\)
On sait que : \[f'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{v(x)^2}\]
Ensuite, on développe le numérateur (mais pas le dénominateur !)
Question 4
Etudier le signe de \(f'(x)\).
Etude du signe de la dérivée :
Il est clair que pour tout \(x\) appartenant à \(D\), on a \(f'(x) > \)0.
Question 5
Dresser le tableau de variations de \(f\).
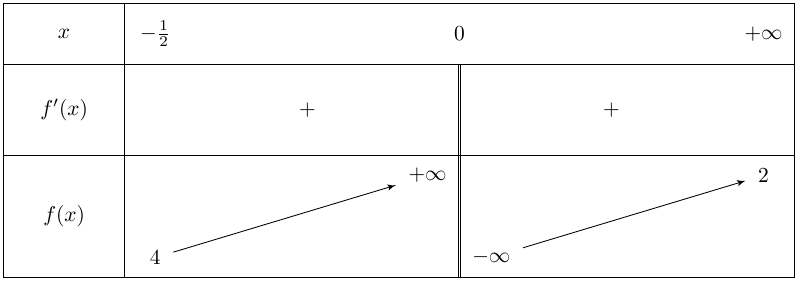
Question 6
Préciser l'équation de la tangente \(T\) à \(C_f\) au point d'abscisse \(\dfrac{1}{2}\).
Construire \(T\) et \(C_f\).
La tangente \(T\) à \(C_f\) au point d'abscisse \(\dfrac{1}{2}\) a pour équation :
\(y=f'\left(\dfrac{1}{2}\right)\left(x-\dfrac{1}{2}\right)+f\left(\dfrac{1}{2}\right)\)
Avec : \(f\left(\dfrac{1}{2}\right)=0\) et \(f'\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{\dfrac{1}{2}}\right)^2=4\)
Donc on a :
\(y=4\left(x-\dfrac{1}{2}\right)\)
\(y=4x-2\)
La tangente \(T\) à \(C_f\) au point d'abscisse \(\dfrac{1}{2}\) a pour équation \(y=4x-2\).
Graphique :
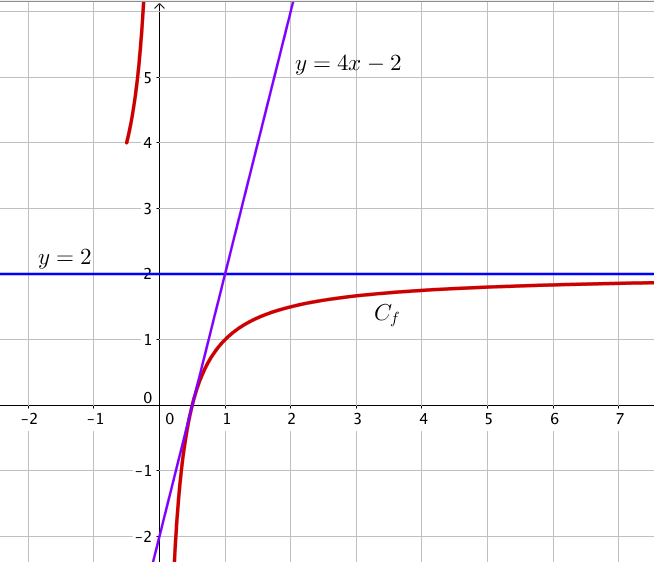
On calcule séparément \(f\left(\dfrac{1}{2}\right)\) et \(f'\left(\dfrac{1}{2}\right)\) . Ensuite on remplace dans la formule du cours donnant l’équation de la tangente.

