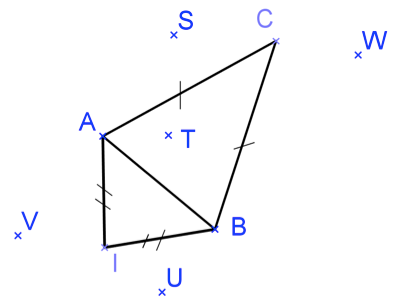
L'énoncé
Coche la ou les bonnes réponse(s) à chacune des questions suivantes.
Tu as obtenu le score de
Question 1
Les points équidistants de \(A\) et de \(B\) sont :
\(S\)
\(C\)
\(T\)
\(I\)
« équidistant » signifie « à égale distance de ».
Lis les codages.
Seulement deux points sont codés à égale distance de \(A\) et de \(B\).
Seuls les points \(C\) et \(I\) sont codés à égale distance de \(A\) et de \(B\) \((CA=CB \text{ et } IA=IB)\) donc ce sont les deux seuls points dont on peut dire qu’ils sont équidistants de \(A\) et de \(B\). (Les bonnes réponses sont les propositions 2 et 4).
Question 2
La médiatrice de \([AB]\) passe par les points :
On ne peut pas savoir.
\(T\)
\(I\)
\(C\)
La médiatrice d’un segment est l’ensemble des points équidistants des extrémités de ce segment.
La médiatrice de \([AB]\) passe donc par les points équidistants de \(A\) et de \(B\).
La médiatrice d’un segment est l’ensemble des points équidistants des extrémités de ce segment donc la médiatrice de \([AB]\) passe par les points équidistants de \(A\) et de \(B\). Elle passe donc par \(I\) et \(C\) : propositions 3 et 4 (d’après les codages et la question précédente).
Question 3
La médiatrice de \([VU]\) passe par les points :
On ne peut pas savoir.
\(I\)
\(C\)
\(T\)
Connaît-on la médiatrice de \([VU]\) ?
Y a-t-il des codages qui permettent de la déterminer ?
Connaît-on des points équidistants de \(V\) et de \(U\) ?
Si rien n’est codé, on ne peut rien affirmer…
On ne connaît pas la médiatrice de \([UV]\), elle n’est pas tracée et aucun codage ne permet de la connaître. Aucun codage ne permet non plus de connaître un point équidistant de \(U\) et de \(V\) donc on ne peut pas savoir.
Question 4
La médiatrice de \([IC]\) passe par les points :
\(I\)
\(A\)
\(B\)
On ne peut pas savoir.
La médiatrice de \([IC]\) est-elle tracée ?
Connaît-on des points équidistants de \(I\) et de \(C\) ?
Attention à bien lire les codages : on cherche des points qui sont à la même distance de \(I\) que de \(C\). Y en a-t-il ?
La médiatrice de \([IC]\) n’est pas tracée. Aucun point de la figure n’est codé à égale distance de \(I\) et de \(C\) donc « on ne peut pas savoir ».
Question 5
La médiatrice de \([AB]\) est la droite :
\((IT)\)
\((UT)\)
\((IC)\)
\((CV)\)
La médiatrice de \([AB]\) est une droite qui passe par ... ?
Elle passe par les points \(I\) et \(C\).
Donc elle s’appelle …
D’après la question 2 la médiatrice de \([AB]\) passe par les points \(I\) et \(C\). Cette médiatrice est donc « la droite qui passe par les points \(I\) et \(C\) » ce qui se note : \((IC)\).