L'énoncé
Pour chacune des questions suivantes, coche la (ou les) phrase(s) qui sont vraie(s).
Tu as obtenu le score de
Question 1
On peut dire que :
\(AOUD\) et \(OBCU\) sont deux carrés de côté 4 cm. 
\(AO=AD\)
\([AO] = [AD]\)
Les deux côtés sont de même longueur : mais attention, les segments eux, ne sont pas égaux ! Pour qu’ils le soient, il faudrait qu’ils soient confondus.
\(BC=OU=4\ cm\)
Comme \(OBCU\) est un carré, on peut dire que \(BC=OU= 4\ cm \).
\(OU=OG\)
Rien n’indique que les longueurs \(OU\) et \(OG\) soient égales, sinon, ce serait codé sur la figure.
Dans cette question, on utilise l’information « \(AOUD\) et \(OBCU\) sont deux carrés de côté 4 cm ».
Un carré possède quatre côtés de même longueur.
Attention, les longueurs sont égales, mais pas les segments : choisis bien la notation correcte !
Choisis bien tes notations : pour parler des longueurs, on peut écrire que \(BC= 4\ cm\), mais il n’est pas correct d’écrire que \([BC]= 4\ cm\).
Question 2
Le quadrilatère en rose sur la figure peut se nommer :
\(AOUD\) et \(OBCU\) sont deux carrés de côté 4 cm.
\(OLUG\)
En partant de \(O\) et en tournant vers la droite, on obtient le nom : \(OLUG\).
\(GOLU\)
En partant de \(G\) et en partant vers le haut, on obtient le nom : \(GOLU\).
\(GLOU\)
En partant de \(G\), il faudrait traverser la figure pour aller à \(L\) : le nom \(GLOU\) n’est pas correct.
\(GULO\)
En partant de \(G\) et en tournant vers le bas, on obtient le nom : \(GULO\).
On tourne autour de la figure, sans la traverser !
Question 3
On peut dire que :
\(AOUD\) et \(OBCU\) sont deux carrés de côté 4 cm.
\([OG]\) est une diagonale du carré \(AOUD\).
\([OG]\) n’est pas une diagonale du carré \(AOUD\) : une diagonale de \(AOUD\) serait plutôt \([AD]\).
\([OG]\) n’est pas une diagonale du carré \(AOUD\).
\([OG]\) n’est pas une diagonale du carré \(AOUD\) !
\([OG]\) est un côté du quadrilatère \(OLUG\).
Dans le quadrilatère \(OLUG, [OG]\) est bien un côté.
\([OG]\) n’est pas un côté du quadrilatère \(OLUG\).
Si !
Une diagonale traverse la figure et joint deux sommets du quadrilatère.
\(G\) est-il un sommet du carré \(AOUD\) ?
Dans ce type d’exercice, prends bien le temps d’observer la figure et de repérer les quadrilatères qui apparaissent dans les questions.
Question 4
On peut dire que :
\(AOUD\) et \(OBCU\) sont deux carrés de côté 4 cm.
\(OM=MU=MG\)
Comme les trois segments \([OM], [MU]\) et \( [MG]\) n’ont pas le même codage, les longueurs ne sont pas égales.
\(M\) est le milieu de \([OU]\).
Avec le codage, on a \(OM=MU\).
\(M\) est le milieu de \([GL]\).
Grâce au codage, on voit que les longueurs \(GM\) et \(ML\) sont égales, donc \(M\) est bien le milieu de \([GL]\).
Les diagonales de \(OLUG\) se coupent en leurs milieux.
Les diagonales de \(OLUG\) sont les segments \([OU]\) et \([GL]\) : elles se coupent en \(M\) qui est aussi leur milieu ! Donc on peut bien dire que les diagonales de \(OLUG\) se coupent en leurs milieux.
Utilise le codage de l’énoncé : deux segments ayant le même codage ont forcément la même longueur.
Par exemple, \([OM]\) et \([MU]\) ont tous les deux des petits tirets verts : ils ont la même longueur.
Le segment \([MG]\) a-t-il le même codage que les deux autres (\([OM]\) et \([MU\)]) ?
Question 5
On peut dire que :
\(AOUD\) et \(OBCU\) sont deux carrés de côté 4 cm.
Le quadrilatère \(DCAB\) est un rectangle.
Pour \(DCAB\), tu vois que l’ordre des lettres ne convient pas.
Le quadrilatère \(DCBA\) est un rectangle.
Oui, c'est bien le bon ordre !
Le quadrilatère \(OLUG\) est un losange.
Oui.
Le quadrilatère \(OLUG\) n’est pas un losange.
Faux !
Sois vigilant(e) à l’ordre des lettres lorsque l’on te donne un quadrilatère !
C’est toujours la même chose : tu dois tourner autour de la figure, et ne pas la traverser…
Si un quadrilatère possède des diagonales qui se coupent en leurs milieux et sont perpendiculaires, alors c’est un … ?
Pour justifier que \(DCBA\) est un rectangle, on peut dire que, \(DCBA\) possède quatre angles droits car \(AOUD\) et \(OBCU\) sont des carrés (donc ils ont tous les deux des angles droits).
Pour justifier que \(OLUG\) est un losange, on peut dire que : \(OLUG\) possède des diagonales qui se coupent en leurs milieux et sont perpendiculaires : d’après le cours, c’est forcément un losange !
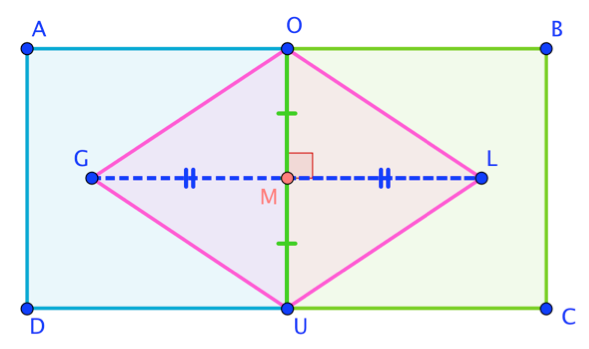
Comme \(AOUD\) est un carré, on peut dire que \(AO=AD\).