L'énoncé
Complète au fur et à mesure la figure suivante. A chaque fois qu’on te parle d’une droite ou d’un point, tu dois le tracer.
Question 1
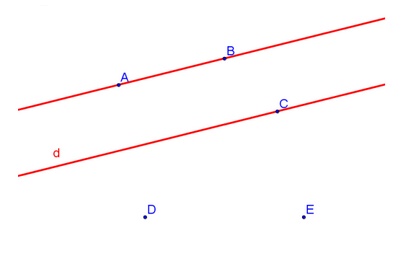
Trace en rouge \((AB)\) et sa parallèle passant par \(C\). Note cette droite \(d\).
Commence par tracer \((AB)\).
Tu dois tracer une parallèle à \((AB)\) qui passe par \(C\).
Pour cela utilise ton équerre et ta règle comme tu as vu en classe.
Question 2
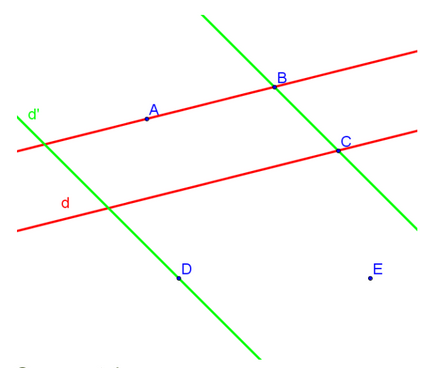
Trace en vert \((BC)\) et sa parallèle passant par \(D\). Note cette droite \(d\mbox\).
Commence par tracer \((BC)\).
Tu dois tracer une parallèle à \((BC)\) qui passe par \(D\).
Pour cela utilise ton équerre et ta règle comme tu as vu en classe.
Question 3
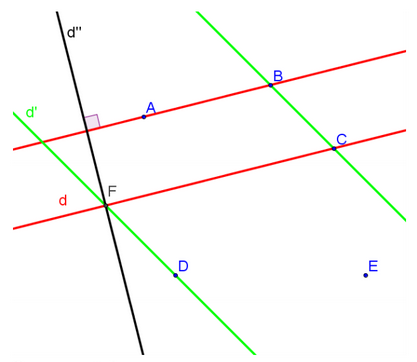
Les droites \(d\) et \(d\mbox\) se coupent en \(F \). Trace à présent en noir la droite \(d\mbox\mbox\), perpendiculaire à \((AB)\) et passant par \(F\).
La droite \(d\mbox’\mbox’\) est perpendiculaire à \((AB)\). Tu vas avoir besoin de ton équerre.
Cette droite doit passer par \(F\).
N’oublie pas de coder l’angle droit.
Question 4
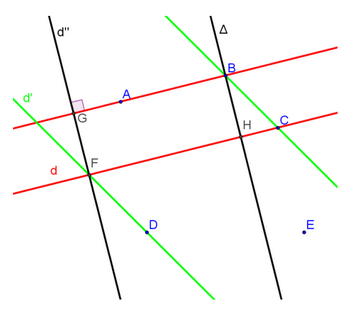
\((AB)\) et \(d\mbox\mbox\) se coupent en \(G\). Trace à présent en noir la droite \(\Delta\) parallèle à \(d\mbox\mbox\) et passant par \(B\). Cette droite coupe \(d\) en \(H\).
Question 5
Que peut-on dire du quadrilatère \(BHFG\) ? Essaye de donner une vraie preuve en rédigeant une phrase.
\((AB)\) et \(d\) sont parallèles donc la droite \(d\mbox\mbox\) qui est perpendiculaire à \((AB)\) est aussi perpendiculaire à \(d\). On peut placer un premier angle droit sur la figure en \(F\).
\(\Delta\) et \(d\mbox\mbox\) sont parallèles donc comme \(d\mbox\mbox\) est perpendiculaire à \((AB)\), \(\Delta\) est aussi perpendiculaire à \((AB)\). On peut placer un autre angle droit sur la figure en \(B\).
\(BHFG\) a trois angles droits donc cest un rectangle.
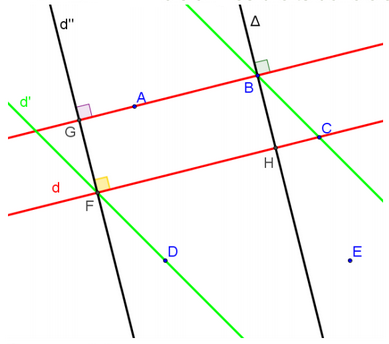
Comment sont les droites de même couleur dans cette figure ?
On sait aussi que \(d\) et \(d\mbox’\mbox’\) sont perpendiculaires.
Saurais-tu trouver d’autres angles droits ?
Question 6
Peut-on utiliser les points \(D\), \(E\) et d'autres points de la figure pour former un rectangle ?
La droite \((DE)\) n'est parallèle à aucune autre droite de la figure donc on ne peut pas former de rectangle avec ces deux points. Tu peux t'en convaincre avec ta règle et ton équerre. On pourrait le prouver avec un quadrillage.
Il faudrait une droite parallèle à \((DE)\) dans la figure.