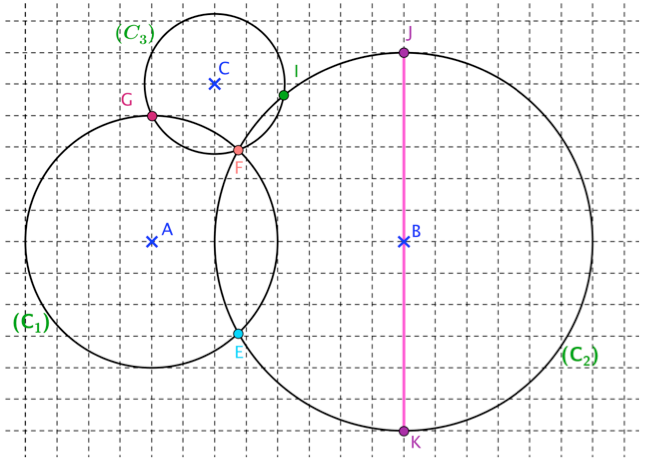
L'énoncé
Coche la ou les bonne(s) réponse(s).
Tu as obtenu le score de
Question 1
\([EF]\) est :
Un diamètre commun aux cercles \((C_1)\) et \((C_2)\).
Une corde commune aux cercles \((C_1)\) et \((C_2)\).
Un arc du cercle.
Une corde du cercle \((C_3)\).
A quel(s) cercle(s) appartiennent les points \(E\) et \(F\) ?
Le segment \([EF]\) ne passe pas par le centre du cercle…
Lorsqu’un segment relie deux points du cercle, sans passer par le centre, c’est une corde du cercle.
Les points \(E\) et \(F\) appartiennent au cercle \((C_1)\), et le segment \([EF]\) ne passe pas par le centre de ce cercle, c’est donc une corde de \((C_1)\).
De même, \([EF]\) est une corde de \((C_2)\).
On peut donc bien dire que c’est une corde commune aux cercles \((C_1)\) et \((C_2)\) ! Proposition 2 vraie.
Question 2
La longueur \(BI\) est égale à :
La longueur \(BF\).
La longueur \(BA\).
La longueur \(BE\).
La moitié de la longueur \(KJ\).
\([BI]\) est un rayon du cercle \((C_2)\) ! Et tous les rayons ont la même longueur…
\(B\) est le centre du centre et \(F\) est sur le cercle : la longueur \(BF\) est aussi égale au rayon !
\([KJ]\) est un diamètre du cercle \((C_2)\).
On a \(BI=BF=BE\) : on a ici trois rayon du cercle \((C_2)\). Propositions 1 et 3 vraies.
Comme \(A\) n’appartient pas au cercle \((C_2)\), \(BI\) n’est pas égale à \(BA\). Proposition 2 fausse.
\([KJ]\) est un diamètre du cercle \((C_2)\): donc, comme le rayon mesure la moitié d’un diamètre, on a bien : \(BI=\frac{1}{2}KJ \) Proposition 4 vraie.
Question 3
Le segment \([AF]\) :
Est un rayon du cercle \((C_1)\).
Est une corde de \((C_1)\).
Est un rayon du cercle \((C_3)\).
Est une corde de \((C_3)\).
Le rayon ne devrait plus avoir de secret pour toi…
Quel est le centre de \((C_1)\) ? \(F\) appartient-il à ce cercle ?
Une corde relie deux points du cercle.
Un rayon ne peut pas être une corde…
Est-il possible que ce soit une corde de \((C_3)\) : le point \(A\) est-il sur ce cercle \((C_3)\) ?
\([AF]\) est un rayon du cercle \((C_1)\). Propositions 1 vraie et 2 fausse.
\([AF]\) ne peut pas être une corde de \((C_3)\) car \(A\) n’appartient pas au cercle \((C_3)\) : ça ne peut pas être une corde (ni un rayon) !
Question 4
Les trois cercles se coupent en :
\(G\)
\(F\)
\(I\)
\(E\)
Il faut ici trouver le point qui appartient aux trois cercles : observe la figure soigneusement.
A quels cercles appartient le point \(G\) ?
\(G\) appartient à \((C_1)\) et \((C_3)\), mais pas à \((C_2)\) : ce n’est pas la bonne réponse. Recommence avec les autres points proposés.
A quels cercles appartient le point \(F\) ?
Le point \(F\) appartient à \((C_1), (C_2)\) et \((C_3)\) : les trois cercles se coupent bien en \(F\). Proposition 2 juste.
Les trois autres réponses ne sont pas bonnes :
- \(G\) appartient à \((C_1)\) et \((C_3)\), mais pas à \((C_2)\).
- \(I\) appartient à \((C_2)\) et \((C_3)\), mais pas à \((C_1)\).
- \(E\) appartient à \((C_1)\) et \((C_2)\), mais pas à \((C_3)\).
Aucun de ces points n’est sur les trois cercles en même temps ! Propositions 1, 3 et 4 fausses.
Question 5
Le triangle \(CFI\) :
Possède deux côtés de même longueur.
Est un triangle isocèle.
Est un triangle quelconque.
Possède un angle droit.
Les trois côtés de \(CFI\) sont : \([CF], [CI] \) et \([FI]\). Lesquels ont la même longueur ?
\([CF]\) et \([CI]\) sont deux rayons, donc…
\([CF]\) et \([CI]\) sont deux rayons, donc ils ont la même longueur : lorsque un triangle a deux côtés de même longueur, on dit qu’il est isocèle . Propositions 1et 2 vraies.
Ce n’est donc pas un triangle quelconque, et on voit qu’il n’y a pas d’angle droit ici. Propositions 3 et 4 fausses.