Fiche de cours
Le vecteur vitesse : exploitation d'une chronophotographie
I. La chronophotographie
On peut trouver le vecteur vitesse grâce à l’étude d’une chronophotographie.
Définition : la chronophotographie est une succession de photos à un intervalle de temps $\Delta t$ régulier qui sont superposées.
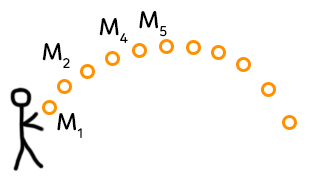
Ce schéma est l’exemple simplifié d’une chronophotographie : un basketteur lance une balle et au fil des photos cette balle bouge et on observe la trajectoire de la balle. 11 photos on été prises pour aboutir à ce résultat, et on ajoute une échelle : ici 1 cm équivaut à à 10 cm dans la réalité et l’intervalle entre chaque photo est de $ \Delta t = 10 \ ms$.
II. Objectif
L’objectif typique dans ce genre de situation est de trouver et de représenter le vecteur vitesse à un endroit donné, ici on cherche $\overrightarrow{v_4}$.
Cette vitesse a trois informations importantes :
Direction : c’est la droite $M_4M_5$, car le vecteur vitesse est colinéaire au point et à son suivant (voir cours vecteur vitesse 1).
Sens : vers la droite.
Norme : on doit la calculer.
III. Calcul de $v_4$
On note $v_4$ la norme du vecteur $\overrightarrow{v_4}$.
Tout d’abord on a $v_4=\dfrac{d}{t}=\dfrac{M_4M_5}{\Delta t}=\dfrac{5 \times 10^{-2}}{10 \times 10^{-3}}=5 \ m/s$ en n’oubliant pas de bien utiliser l’échelle pour ne pas se tromper.
Ensuite, on crée l’échelle des vitesses : par exemple 1 cm équivaut à 1 m/s.
Pour finir, on trace le vecteur $\overrightarrow{v_4}$ sur le schéma en utilisant toutes les informations : direction, sens et norme.
