Fiche de cours
Lien entre $\overrightarrow{v}$ et $\overrightarrow{v}_{moy}$
Il est ici question de faire le lien entre ces deux vitesses, avec pour rappel :
$\overrightarrow{v_{moy}}=\dfrac{\overrightarrow{M(t)M(t+\Delta t)}}{\Delta t}$
On s’intéresse à ces trois schémas décrivant une trajectoire d’une balle lancée :
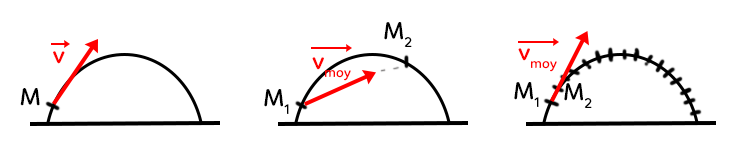
Le trait horizontal représente le sol et la trajectoire est parabolique. Sur le premier schéma, la trajectoire parfaite est tracée : tous les points qui tracent la courbe sont présents, donc le tracé est continu. On peut alors calculer la vitesse en tous points grâce à la première partie du cours : on cherche la tangente à la courbe.
Le deuxième schéma représente la vraie expérience. La balle va bien parcourir la trajectoire parabolique sauf qu’en terme de chronophotographie seules deux positions sont connues : les points $M_1$ et $M_2.$ On voit ainsi que $\overrightarrow{v}_{moy}$ est éloigné de la vitesse $\overrightarrow{v}$ trouvée sur le premier schéma.
Le dernier schéma représente une amélioration du second schéma : on prend plus de photos de la trajectoire de la balle. On capte alors beaucoup plus de positions de l’objet. La précision est beaucoup plus grande car les photos sont prises avec un intervalle de temps beaucoup plus petit. Le vecteur $\overrightarrow{v}_{moy}$ est alors beaucoup plus proche du vecteur vitesse $\overrightarrow{v}$.
Conclusion
Si $\Delta t$ est très faible devant la durée typique du mouvement, alors $\overrightarrow{v}$ et $\overrightarrow{v}_{moy}$ sont quasiment identiques. Une durée typique du mouvement ici équivaut au temps que met la balle à atteindre le sol.
