L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
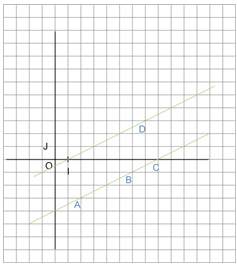
Soit le repère \((O ; I ; J)\).
On considère les points \(A(2 ; - 3), B(6 ; - 1), C(8 ; 0), D(7 ; 3)\).
Calculez les coordonnées de \(\overrightarrow{AB}\) et \(\overrightarrow{BC}\).
\(\overrightarrow{AB}(4 ; 2)\) et \(\overrightarrow{BC}(2 ; 1)\)
\(\overrightarrow{AB}(8 ; -4)\) et \(\overrightarrow{BC}(14 ; -1)\)
\(\overrightarrow{AB}(4 ; -2)\) et \(\overrightarrow{BC}(7 ; -0,5)\)
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous la formule des coordonnées d'un vecteur ? \(\overrightarrow{AB}(x_B - x_A ; y_B - y_A)\)
Question 2
On a : \(\overrightarrow{AB}(4 ; 2)\) et \(\overrightarrow{BC}(2 ; 1)\)
Les points \(A\), \(B\) et \(C\) sont-ils alignés ?
Oui, car \(\overrightarrow{AB}= \dfrac{1}{2} \overrightarrow{BC}\).
Non.
Oui, car \(\overrightarrow{AB} = 2\overrightarrow{BC}\).
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous la condition sur les vecteurs pour que trois points soient alignés ? C’est dans votre cours.
Il faut par exemple que \(\overrightarrow{AB}\) et \(\overrightarrow{BC}\) soient colinéaires.
Besoin d’un rappel ? Allez voir la vidéo dans les prérequis.
Question 3
\(I(0 ; 1)\)
\(I(1 ; 1)\)
\(I(0 ; 0)\)
Aucune des trois réponses précédentes n’est exacte.
Faites une figure.
\(I\) est sur l’axe des abscisses. \(\overrightarrow{OI}\) est le vecteur unité.
Question 4
\(A(2 ; - 3), B(6 ; - 1), C(8 ; 0), D(7 ; 3)\).
On connaît les coordonnées de \(\overrightarrow{AB}\). Calculez les coordonnées de \(\overrightarrow{ID}\).
\(\overrightarrow{AB} (4 ; 2)\) et \(\overrightarrow{ID} (-6 ; -3)\)
\(\overrightarrow{AB} (4 ; 2)\) et \(\overrightarrow{ID} (7 ; 2)\)
\(\overrightarrow{AB} (4 ; 2)\) et \(\overrightarrow{ID} (6 ; 3)\)
Aucune des trois réponses précédentes n’est exacte.
C’est la même formule que pour la question n°1.
Question 5
On sait que \(\overrightarrow{AB} (4 ; 2)\) et \(\overrightarrow{ID} (6 ; 3)\)
Les droites \((AB)\) et \((ID)\) sont-elles parallèles ?
Oui, car \(\overrightarrow{ID}=\dfrac{3}{2} \times \overrightarrow{AB}\).
Non.
Oui, car \(\overrightarrow{ID}=\dfrac{2}{3} \times \overrightarrow{AB}\).
Aucune des trois réponses précédentes n’est exacte.
Demandez-vous si les vecteurs sont colinéaires.
Besoin d’un rappel sur la méthode ? Regardez la vidéo dans les prérequis.
Question 6
Sachant que Les droites \((AB)\) et \((ID)\) sont parallèles, peut-on en déduire la nature du quadrilatère \(ABDI\) ?
C’est un parallélogramme.
C’est un trapèze.
C’est un trapèze rectangle.
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous un quadrilatère ayant deux côtés parallèles ?
Le quadrilatère \(ABDI\) a t-il d'autres propriétés ?
Question 7
Soit le repère \((O ; I ; J)\).
On considère les points : \(A(- 2 ; 2), B(4 ; - 1), C(0 ; 1)\).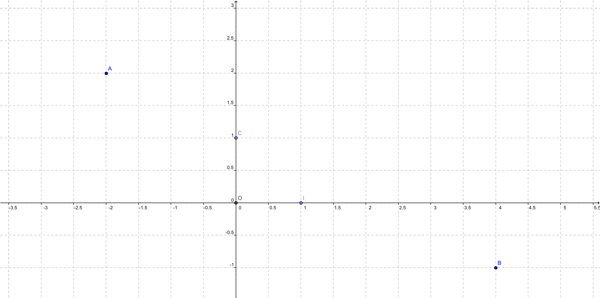
Calculez les coordonnées de \(\overrightarrow{OB} +2 \times \overrightarrow{AC}\).
\(\overrightarrow{OB}+2 \times \overrightarrow{AC}\) a pour cordonnées \((8 ; -3)\)
\(\overrightarrow{OB}+2 \times \overrightarrow{AC}\) a pour cordonnées \((0 ; -6)\)
\(\overrightarrow{OB}+2 \times \overrightarrow{AC}\) a pour cordonnées \((-8 ; 3)\)
Aucune des trois réponses précédentes n’est exacte.
Savez-vous trouver les coordonnées de la somme de deux vecteurs ? Un petit rappel : regardez la vidéo.
Question 8
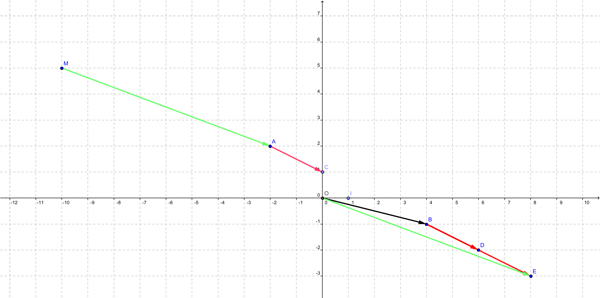
Soit \( M (x ; y)\) vérifiant \(\overrightarrow{MA}=\overrightarrow{OB}+2 \times \overrightarrow{AC}\).
Sachant que \(\overrightarrow{OB}+2 \times \overrightarrow{AC}\) a pour cordonnées \((8 ; -3)\), déterminez les coordonnées de \(M\).
\(M(- 1 ; 5)\)
\(M(- 10 ; 5)\)
\(M(10 ; -5)\)
Aucune des trois réponses précédentes n’est exacte.
Deux vecteurs sont égaux, si et seulement si leurs coordonnées sont égales.
Question 9

Soit \( N (x ; y)\) vérifiant \(3 \times \overrightarrow{AN}-\overrightarrow{BN}=0\).
Les coordonnées de \(N\) vérifient le système suivant :
\(\left\{ \begin{array}{rcl} 3(x+(-2))-(x-4)=0 \\ 3(y+2)-(y-(-1)) = 0 \end{array}\right.\)
\(\left\{ \begin{array}{rcl} 3(x+(-2))-(x+4)=0 \\ 3(y+2)-(y+(-1)) = 0 \end{array}\right.\)
\(\left\{ \begin{array}{rcl} 3(x-(-2))-(x-4)=0 \\ 3(y-2)-(y-(-1)) = 0 \end{array}\right.\)
Aucune des trois réponses précédentes n’est exacte.
Traduisez cette égalité vectorielle par un système de deux équations à deux inconnues.
Pour cela, il vous faudra exprimer les coordonnées de \(\overrightarrow{AN}\) et de \(\overrightarrow{BN}\).
Question 10

Résolvez le système suivant et trouvez les coordonnées de N :
\(\left\{ \begin{array}{rcl} 3(x-(-2))-(x-4)=0 \\ 3(y-2)-(y-(-1)) = 0 \end{array}\right.\)
\(N\left(-5 ; \dfrac{7}{2}\right)\)
\(N\left(-5 ; -\dfrac{7}{2}\right)\)
\(N\left(5 ; - \dfrac{7}{2}\right)\)
Aucune des trois réponses précédentes n’est exacte.
Il vous suffit de résoudre le système précédent.
Besoin d’un rappel sur les systèmes ? Allez voir la vidéo dans les prérequis.