Fiche de cours
Translations et vecteurs
Définition
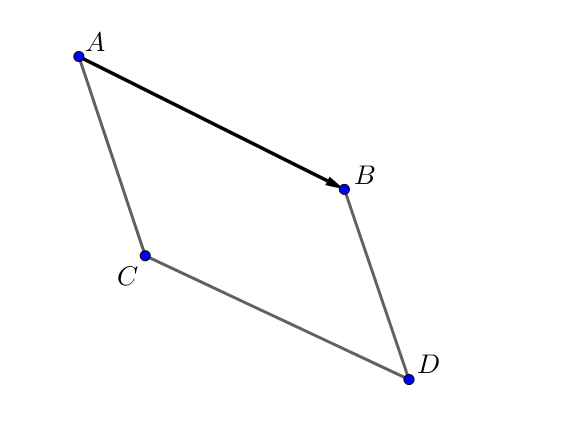
La translation qui transforme $A$ en $B$ est l'unique transformation qui transforme un point $C$ en un point $D$ tel que $ABDC$ soit un parallélogramme ou bien tel que $[AD]$ et $[BC]$ ont même milieu.
La translation peut également être vue comme un glissement de $A$ vers $B$ : ce glissement s'effectue selon une certaine direction, avec un certain sens et selon une certaine longueur.
On passe donc de $A$ vers $B$ par la translation de vecteur $\overrightarrow{AB}$ et de $C$ vers $D$ par la même translation.
Cette translation est notée $t_{\overrightarrow{AB}}$.
Le fait de passer du point $A$ au point $B$ par la translation de vecteur $\overrightarrow{AB}$ revient à écrire que l'image de $A$ par la translation de vecteur $\overrightarrow{AB}$ est $B$ : $t_{\overrightarrow{AB}}(A) = B$.
De même, le point $C$ est transformé en point $D$ par la translation de vecteur $\overrightarrow{AB}$ ce qui s'écrit $t_{\overrightarrow{AB}}(C) = D$.
Vecteurs égaux
Suppo
