L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
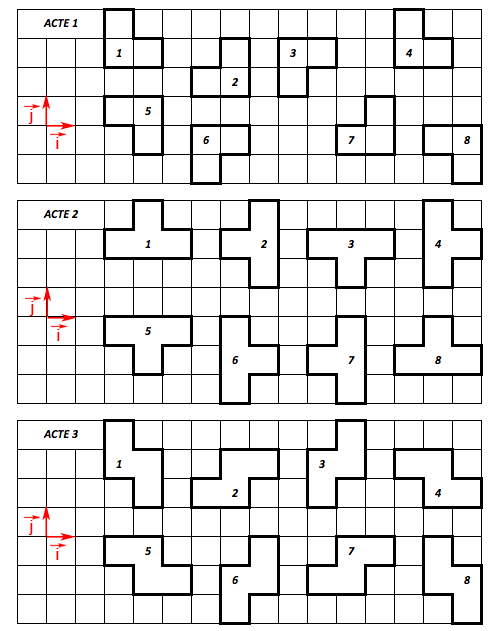
Acte 1 : La figure 4 est l'image de la figure 1 par le « glissement » de 10 carreaux vers l'Est. On parle de translation de vecteur \(10\overrightarrow{i}\) où \(\overrightarrow{i}\) est le vecteur unitaire de l'axe horizontal.
On note désormais \((\overrightarrow{i};\overrightarrow{j})\) un couple de vecteurs unitaires comme représenté sur la figure. Quelles couples de figures sont liés par une translation ?
On notera les couples sous la forme (F4 ; F1) pour (Figure 4, Figure 1).
(F6 ; F3) et (F2 ; F7) et (F5 ; F7)
(F6 ; F3) et (F2 ; F7) et (F1 ; F7)
(F6 ; F3) et (F2 ; F7) et (F5 ; F8)
Aucune des trois réponses précédentes n’est exacte.
Deux figures sont liées par une translation si on obtient l’une par un « glissement » de l’autre.
Besoin d’un rappel sur cette notion ? Allez voir la vidéo dans les prérequis.
Question 2
Acte 2 : La figure F8 est l'image de la figure F1 par une translation.
Quel est le vecteur de la translation?
\(10\overrightarrow{i}-4\overrightarrow{j}\)
\(10\overrightarrow{i}+4\overrightarrow{j}\)
\(-10\overrightarrow{i}-3\overrightarrow{j}\)
Aucune des trois réponses précédentes n’est exacte.
Suivez tout simplement le chemin d’un point de la figure 1 pour rejoindre le même point de la figure 8.
On travaille avec des déplacements horizontaux et verticaux uniquement.
Question 3
Acte 3 : La figure F5 est l'image de la figure F4 par une translation.
Quel est le vecteur de cette translation?
\(-10\overrightarrow{i}-4\overrightarrow{j}\)
\(10\overrightarrow{i}+4\overrightarrow{j}\)
\(-10\overrightarrow{i}-3\overrightarrow{j}\)
Aucune des trois réponses précédentes n’est exacte.
C’est le même travail qu’à la question précédente.
Question 4
Acte 3 : La figure F2 est l'image de la figure F7 par la translation de vecteur :
\(-3\overrightarrow{i}-4\overrightarrow{j}\)
\(3\overrightarrow{i}+4\overrightarrow{j}\)
\(-4\overrightarrow{i}+3\overrightarrow{j}\)
Aucune des trois réponses précédentes n’est exacte.
C’est le même travail qu’à la question précédente.