Fiche de cours
Trigonométrie - Les valeurs à connaître
Pour rappel, le cosinus d'un angle correspond à l'abscisse du point sur le cercle associé et le sinus correspond à l'ordonnée du point.
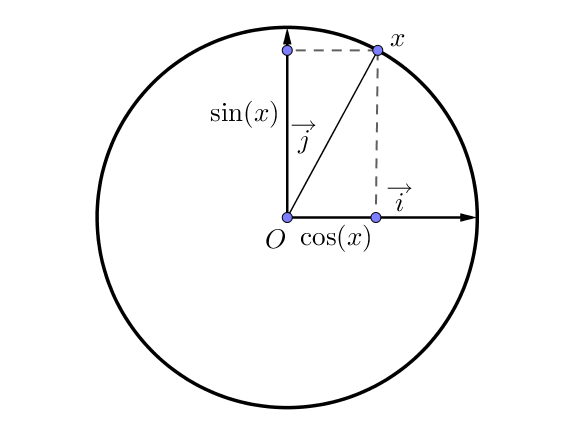
Lorsque l'angle vaut $0°$, on a $\cos(0) = 1$ et $\sin(0) = 0$.
Lorsque l'angle vaut $90°$ ou $\dfrac{\pi}{2}$ radians, on a $\cos(90) = 0$ et $\sin(90) = 1$.
Lorsque l'angle vaut $180°$ ou $\pi$ radians, on a $\cos(180) = -1$ et $\sin(180) = 0$.
Les mesures précédentes peuvent se retrouver par lecture graphique.
Lorsque l'angle vaut $45°$ ou $\dfrac{\pi}{4}$ radians, on a $\cos(45) = \dfrac{\sqrt{2}}{2}$ et $\sin(45) = \dfrac{\sqrt{2}}{2}$, qu'il faut retenir par coeur.
Dans ce cas, le cosinus et le sinus sont égaux: en effet, l'angle est situé sur l'axe de symétrie d'équation $y =x$.
Graphiquement, on trouve que le sinus de l'angle $30°$ ou encore $\dfrac{\pi}{6}$ vaut $0,5$.
On en déduit alors que le cosinus vaut $\dfrac{\sqrt{3}}{2}$ (car $\cos(30)^2 + \sin(30)^2 = 1$).
