L'énoncé
Cet exercice est un QCM ; il n’y a qu’une seule bonne réponse possible parmi toutes celles proposées.
Tu as obtenu le score de
Question 1
On tire au hasard une carte dans un jeu de 32 cartes. Quelle est la probabilité de ne pas tirer un carreau ?
\(p = \dfrac{1}{4}\)
\(p = \dfrac{3}{4}\)
\(p = \dfrac{1}{2}\)
On ne peut pas savoir.
"Ne pas tirer un carreau" est l'événement contraire de "tirer un carreau".
Quelle est la probabilité de "tirer un carreau" ?
Quelle est alors la probabilité de "ne pas tirer un carreau" ?
Question 2
On lance deux dés équilibrés. La probabilité d'obtenir un double 6 est :
\(p = \dfrac{2}{3}\)
\(p = \dfrac{4}{36}\)
\(p = \dfrac{1}{2}\)
\(p = \dfrac{1}{36}\)
Il y a 36 issues possibles au total, et un seul double 6 !
Quelles sont les 36 issues possibles ?
Combien d'entres elles donnent un double 6 ?
Question 3
\(A\) et \(B\) sont deux événements incompatibles tels que \(p(A) = 0,43\) et \(p(B) = 0,15\). Alors :
\(p(A \cup B) = 0,0645\)
\(p(A \cup B) = 0,58\)
Comme \(A\) et \(B\) sont incompatibles on a \(A \cap B = \emptyset\) et donc \(p(A \cap B) = 0\).
Alors \(p(A \cup B) = p(A)+p(B)=0,43+0,15=0,58\).
\(p(A \cup B) = 0,28\)
On ne peut pas savoir.
D'après le cours quelle est la formule de \(p(A \cup B)\) ?
Quelle est la définition de deux événements incompatibles ?
Que vaut alors \(p(A \cap B)\) ?
Question 4
Un sac contient les cinq jetons suivants :
On choisit un jeton au hasard ; on considère les événements suivants :
\(A\) : "le numéro porte un numéro pair".
\(B\) : "le jeton est vert".
\(C\) : "le jeton est rouge".
\(D\) : "le jeton porte le numéro 1".
\(p(B) = \dfrac{2}{10}\)
\(p(C \cap D) = \dfrac{4}{10}\)
\(p(C \cup D) = \dfrac{3}{5}\)
\(p(A) = 0\)
C’est la seule réponse possible !
Combien de jetons sont verts ? Donc que vaut \(p(B)\) ?
\(C \cap D\) : "le jeton est rouge et porte le numéro 1". Combien de jetons sont rouges et portent le numéro 1 ? Donc que vaut \(p(C \cap D)\) ?
\(C \cup D\) : "le jeton est rouge ou porte le numéro 1". Combien de jetons sont soient rouges, soient portent le numéro 1 ? Donc que vaut \(p(C \cup D)\) ?
Combien de jetons portent un numéro pair ? Donc que vaut \(p(A)\) ?
Question 5
On considère une urne contenant sept billes rouges numérotées 1, 2, 3, 4, 5, 6, 7 et quatre billes vertes numérotées 8, 9, 10, 11.
On tire au hasard une bille de l'urne.
Quelle est la probabilité de tirer une bille rouge ?
\(\dfrac{1}{2}\)
\(\dfrac{7}{11}\)
\(\dfrac{3}{4}\)
On ne peut pas savoir.
Combien y a-t-il de billes rouges ?
Combien y a-t-il de billes en tout ?
Conclure.
Question 6
On considère une urne contenant sept billes rouges numérotées 1, 2, 3, 4, 5, 6, 7 et quatre billes vertes numérotées 8, 9, 10, 11.
On tire au hasard une bille de l'urne.
Quelle est la probabilité de tirer une bille rouge portant un numéro impair ?
\(\dfrac{4}{11}\)
En effet, il y a 4 billes rouges ET portant un numéro impair sur un total de 11 billes.
\(\dfrac{1}{4}\)
\(\dfrac{4}{7}\)
On ne peut pas savoir.
Il s'agit ici de la probabilité d'une intersection. On veut des billes rouges ET portant un numéro impair.
Combien y a-t-il de billes rouges ? Combien d'entre elles ont un numéro impair ?
Combien y a-t-il de billes en tout ? Conclure.
Question 7
On considère une urne contenant sept billes rouges numérotées 1, 2, 3, 4, 5, 6, 7 et quatre billes vertes numérotées 8, 9, 10, 11.
On tire au hasard une bille de l'urne.
Quelle est la probabilité de tirer une bille verte ou portant un numéro pair ?
\(\dfrac{2}{11}\)
\(\dfrac{5}{11}\)
\(\dfrac{7}{11}\)
On pose \(V\) = « la bille tirée est verte », et \(P\) = « la bille tirée porte un numéro pair ».
On a \(p(V) = \dfrac{4}{11}\) et \(p(P) = \dfrac{5}{11}\).
Alors \(p(P \cap V) = \dfrac{2}{11}\).
Donc : \(p(P \cup V) = p(P)+p(V)-p(P \cap V) = \dfrac{4+5-2}{11} = \dfrac{7}{11}\)
On ne peut pas savoir.
Il s'agit ici de la probabilité d'une réunion. On veut des billes vertes OU des billes portant un numéro pair.
Combien y a-t-il de billes vertes ?
Combien y a-t-il de billes portant un numéro pair ?
Combien y a-t-il de billes vertes ou de billes portant un numéro pair ? Conclure.
On peut aussi chercher \(p(V \cup\) Pair) en appliquant la formule du cours.
Question 8
On fait tourner la roue équilibrée ci-contre ; on lit le numéro en face du repère.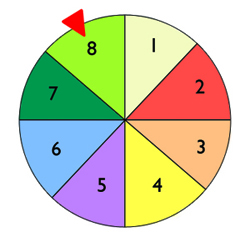
On considère les événements \(A\) et \(B\) :
\(A\) : "le numéro est strictement supérieur à 4".
\(B\) : "le numéro est impair".
Quelle est la probabilité de l'événement \(A \cap B\) ?
\(\dfrac{1}{8}\)
\(\dfrac{1}{4}\)
Il y a 2 numéros strictement supérieurs à 4 ET impairs sur un total de 8 numéros.
Alors \(p(A \cap B) = \dfrac{2}{8} = \dfrac{1}{4}\).
\(\dfrac{1}{2}\)
On ne peut pas savoir.
Il s'agit ici de la probabilité d'une intersection.
Combien de numéros sont strictement supérieur à 4 ET impair ?
Combien y a-t-il de numéros en tout ? Conclure.
Question 9
\(A\) : "le numéro est strictement supérieur à 4".
\(B\) : "le numéro est impair".
La probabilité de l'événement \(A \cup B\) est :
\(\dfrac{3}{4}\)
En effet, \(p(A) = \dfrac{4}{8}\) et \(p(B) = \dfrac{4}{8}\), et aussi \(p(A \cap B) = \dfrac{2}{8}\)
Alors \(p(A \cup B) = p(A)+p(B)-p(A \cap B) = \dfrac{4}{8}+\dfrac{4}{8}-\dfrac{2}{8}=\dfrac{6}{8}=\dfrac{3}{4}\)
\(\dfrac{1}{2}\)
1
On ne peut pas savoir.
Il s'agit ici de la probabilité d'une réunion.
Combien de numéros sont strictement supérieur à 4 OU de numéros impairs ?
Combien y a-t-il de numéros en tout ? Conclure.
Question 10
\(A \): "le numéro est strictement supérieur à 4".
Quelle est la probabilité de l'événement contraire \(\overline{A}\) ?
\(0\)
\(\dfrac{1}{2}\)
\(p(A) = \dfrac{4}{8} = \dfrac{1}{2}\) donc \(p(\overline{A}) = 1-p(A)=\dfrac{1}{2}\)
\(\dfrac{1}{4}\)
On ne peut pas savoir.
Il s'agit ici de la probabilité d'un événement contraire.
Quelle est la probabilité de \(A\) ?

Posons : \(C\) = « la carte tirée est un carreau » : on a \(p(C) = \dfrac{8}{32} = \dfrac{1}{4}\)
Alors \(p(\overline{C}) = 1 -p(C)=1-\dfrac{1}{4}=\dfrac{3}{4}\)