Fiche de cours
Ensemble des nombres réels $\mathbb{R}$ - Intervalles
Définition
L’ensemble des nombres utilisés au quotidien (les nombres négatifs, positifs, décimaux, …) est appelé l’ensemble des réels, et est noté $\mathbb{R}$.
On peut représenter l’ensemble de ces nombres réels par une droite gradué, munie d'une origine $O$, d'une unité et orientée vers les nombres positifs.
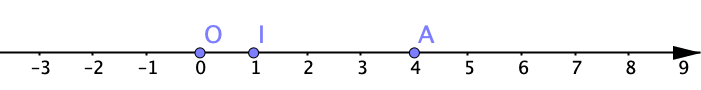
On a placé sur la droite le point $A$ qui correspond au nombre $4$. On dit que $A$ a pour abscisse $4$.
Ainsi, à chaque nombre réel correspond un point sur la droite et réciproquement.
On peut indiquer sur la droite le symbole $+ \infty$, qui est le symbole de l’infini pour signifier que la droite ne s’arrête pas.
Intervalles dans $\mathbb{R}$
On s’intéresse désormais à une partie de la droite, comprise entre $I$ et $A$.
L’ensemble de ces réels compris entre les abscisses des points $I$ et $A$ est appelé un intervalle.
La notation de l’intervalle est la même que pour un segment.
Par exemple, l’intervalle entre les abscisses des points $I$ et $A$ se note $[1; 4]$.
Si l'abscisse du point $I$ n’appartient par à l’intervalle, on utilisera un crochet ouvert pour le signifier.
On notera alors $]1; 4]$.
Il existe différents types d’intervalles.
| Intervalle | Inégalité | Droite |
| $[a; b]$ | $a \leq x \leq b$ | |
| $]a; b]$ | $a < x \leq b$ | |
| $[a; + \infty [$ | $a \leq x$ | |
| $]- \infty; a [$ | $x < a$ |
Pour simplifier l’écriture de certains intervalles, on utilise des notations particulières.
Ainsi, $\mathbb{R}^+$ correspond à l’ensemble des nombres réels positifs, que l’on peut aussi noter $[0; +\infty [$.
$\mathbb{R}^-$ correspond à l’ensemble des nombres réels négatifs, que l’on peut aussi noter $]- \infty; 0]$.
Enfin, $\mathbb{R}^*$ correspond à l’ensemble des nombres réels privés de 0, que l'on note aussi $\mathbb{R} \backslash 0$.
Intersection de deux intervalles $I$ et $J$
L'intersection des intervalles $I$ et $J$ est composé de tous les éléments communs à $I$ et à $J$ en même temps.
On note l’intersection par $I \cap J$ et cela se lit $I$ inter $J$.
Exemples :
1) Déterminons $[-1; 2[ \cap [0; 3]$.
Pour cela, on peut sur la droite graduée hachurer le premier intervalle puis le second intervalle. L’intersection correspond à l’intervalle hachuré deux fois.

On trouve alors $[-1; 2[ \cap [0; 3] = [0; 2[$
2) Déterminons $[1;2] \cap [3; + \infty [$.
On remarque que $2 < 3$, donc aucun élément n'est commun aux deux intervalles.
On dira que l’intersection est égale à l’ensemble vide et se note $ \varnothing$.
Ainsi : $[1;2] \cap [3; + \infty [=\varnothing$

Réunion de deux intervalles $I$ et $J$
La réunion des intervalles $I$ et $J$ est composée de tous les éléments appartenant à $I$ ou à $J$.
La réunion peut aussi contenir des éléments appartenant à la fois à $I$ et à $J$.
La réunion se note $I \cup J$ et se lit $I$ union $J$.
Exemples
1) Déterminons $[-1; 2[ \cup [0; 3]$.
Pour cela, on peut sur la droite graduée hachurer les deux intervalles. La réunion correspond à l’intervalle hachuré au moins une fois.

On trouve alors $[-1; 2[ \cup [0; 3] = [-1; 3]$
2) Déterminons $[1;2] \cup [3; + \infty [$.
On remarque qu’il n’y a pas de simplification possible de l’écriture.
On écrit donc la réunion sous la forme $[1;2] \cup [3; + \infty [$.
