1) Les affirmations suivantes sont-elles vraies ou fausses ? (justifier la réponse)
a) Si $f$ est une fonction définie et strictement croissante sur $[-2 ; 5]$ alors $f(-2) < f(5)$.
b) Si $f$ est une fonction définie sur $[1 ; 4]$ telle que $f(1) > f(4)$ alors $f$ est strictement décroissante sur $[1 ; 4]$.
c) Si $f$ change le sens de toutes inégalités sur $\mathbb{R}$, et $f(-1) = 4$ alors pour tout réel $x\in [-1 ; +\infty [$ on a : $f(x)\leq 4$.
2) Répondre aux questions suivantes en utilisant la courbe représentative $C_f$ de la fonction $f$.
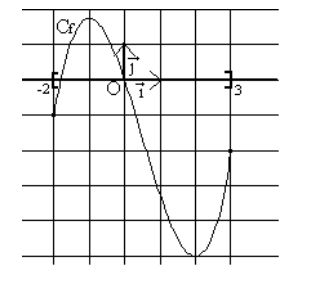
a) Déterminer graphiquement les images de $0$ et $-2$.
b) Déterminer graphiquement le(s) éventuels antécédent(s) de $2; -2$ et $-5$.
c) Sur quel(s) intervalle(s) $f$ est-elle croissante ?
d) Déterminer graphiquement le signe de $f(x)$ (faire un tableau de signe).
1) a) C’est la définition de fonction strictement décroissante qui permet d’affirmer que $f(-2) < f(5)$, donc cette affirmation est vraie.
b) Pas forcément, on peut très bien avoir une fonction telle que $f(1) > f(4)$ et non strictement décroissante,
L’inégalité $f(a) > f(b)$ avec $a < b$ n’est pas vérifiée pour tout couple de réels mais pour $1$ et $4$ donc cette affirmation est fausse.
c) Cette affirmation est vraie.
Si $x\in [-1 ; +\infty [$ on a $x\geq -1$ (avec $x$ et $–1$ appartenant à $[-1 ; +\infty [$) donc
$f(x)\geq f(-1)$ (puisque $f$ change le sens de toutes inégalités sur $[-1 ; +\infty [$), on a donc $f(x)\geq 4$.
2) a) Le point de coordonnées $(0 ; 0$) appartient à $C_f$ donc $f(0) = 0$.
Le point de coordonnées $(-2 ; -1)$ appartient à $C_f$ donc $f(-2) = -1$.
b) La droite d’équation $y = 2$ ne coupe pas $C_f$ donc $2$ n’a pas d’antécédents.
La droite d’équation $y = -2$ coupe $C_f$ en deux points d’abscisses $0,65$ et $3$ (environ),
$-2$ a deux antécédents : $0,65$ et $3$.
La droite d’équation $y = -5$ coupe $C_f$ au point d’abscisse $2$.
$–5$ a donc un antécédent : le nombre $2$.
c) $f$ est croissante sur $[-2;-1]$ et $[2 ;3]$.
d) Tableau de signe de $f(x)$
| x | -2 -1.7 0 3 |
| f(x) | - 0 + 0 - |
