L'énoncé
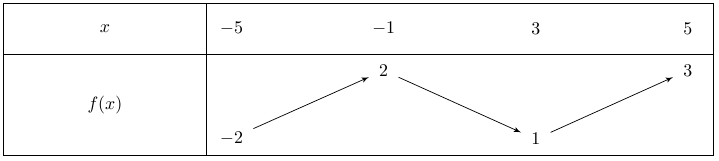
Soit \(f\) une fonction définie sur l’intervalle \([-5;5]\) dont le tableau de variation est le suivant : (on suppose que la courbe représentative de \(f\) sur \([-5;5]\) s’obtient « sans lever le crayon »).
Tu as obtenu le score de
Question 1
Si on note \(C_f\) la courbe représentative de la fonction \(f\) dans un repère, alors\(C_f\) coupe l'axe des abscisses...
En un point.
En deux points.
En trois points.
Autre réponse.
Faites une courbe au brouillon.
Question 2
Le maximum de \(f\) sur \([-5 ; 5]\) est...
2
3
On ne sait pas.
Autre réponse.
La notion de maximum est intuitive. Observez bien votre courbe tracée au brouillon et concluez.
Question 3
Le minimum de \(f\) sur \([-1 ; 5]\) est...
1
-2
On ne peut pas savoir.
Autre réponse.
Attention on a changé d’intervalle ! Je sais, vous l’aviez vu…
Question 4
Sur \([-5 ; 5]\), la fonction \(f\) est...
Croissante.
Décroissante.
Ni l’un ni l’autre.
Autre réponse.
La question repose sur tout l’ensemble de définition de \(f\).
Question 5
Sur \([-1 ; 3]\), la fonction \(f\) est...
Croissante.
Décroissante.
En baisse.
Autre réponse.
Pas de blague ! Observez le sens de la flèche…
Question 6
L'image de 0 est...
Égale à 0.
Négative.
Strictement inférieure à 1.
Autre réponse.
Utilisez encore votre graphique, ça peut vous aider.
Question 7
Combien \(\dfrac{3}{2}\) a-t-il d'antécédents ?
1
3
Aucun.
Autre réponse.
Vous connaissez la valeur de \(\dfrac{3}{2}\) bien sûr…
Question 8
Si \( -5 < b < a < -1 \), alors...
\( f(a) < f(b)\)
\( f(a) > f(b)\)
\( f(a)\) et \(f(b)\) sont négatifs.
Autre réponse
Revoyez votre cours sur la définition d’une fonction croissante. Allez voir la vidéo dans les prérequis.
Question 9
Si \(-1 < b < a < 5\), alors...
\(f(a) < f(b)\)
\(f(a) > f(b)\)
On ne peut pas savoir
Autre réponse
La fonction est-elle monotone sur l’intervalle donné ?
Sur l’intervalle \([-1 ; 5]\) la fonction n’est ni croissante ni décroissante. Elle n’est pas monotone donc on ne peut pas utiliser la propriété du cours sur les fonctions croissantes ou décroissantes. On ne peut donc pas conclure. Pour t’en convaincre, essaye au crayon de tracer plusieurs courbes qui vérifient les informations du tableau de variations. Dans certains cas, \(f(a)\) sera plus grand que \(f(b)\) et réciproquement.
Question 10
Si \(x\) et \(y\) sont deux réels de l'intervalle \([-1;3]\) tels que \(x\) est positif et \(y\) est négatif, alors...
\( f(x) < f(y)\)
\( f(x) > f(y)\)
\( f(x)\) et \( f(y)\) sont de signes opposés
Autre réponse
Qui de \(x\) ou \(y\) est le plus grand ? Essayez avec des nombres au hasard si vous ne savez pas. La réponse est évidente.
