Fiche de cours
Maximum, minimum d'une fonction
Une situation concrète
Soient $f$ et $g$ deux fonctions représentant l'évolution de la température au cours du temps.
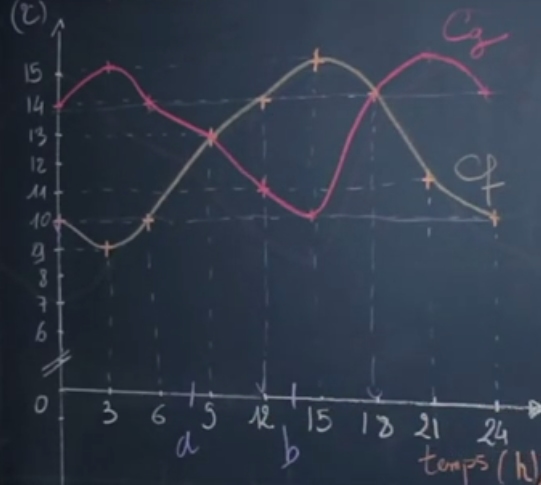
Pour trouver le maximum de $f$, il faut regarder à quel instant la température est maximale. Il est atteint à $t = 15$.
Pour trouver le minimum de $f$, il faut regarder à quel instant la température est minimale. Il est atteint à $t = 3$.
Définition
Soit $f$ une fonction définie sur $D$, son ensemble de définition.
1) $M$ est un maximum de $f$ si pour tout $t \in D$, $f(t) \leq M$.
2) $m$ est un minimum de $f$ si pour tout $t \in D$, $f(t) \geq m$.
En d'autres termes, cette première inégalité signifie que la température est toujours plus petite que $M$ qui est le maximum.
On utilise la variable $t$ car on regarde l'évolution en fonction du temps, mais dans la plupart des cas, la variable utilisée sera $x$ sans que cela change la définition du maximum.
Le maximum de $f$ sur $[0; 24]$ est 15 et il est atteint en $t = 15$.
La température maximale est donc de 15°C et est atteinte à 15h.
Le minimum de $f$ sur $[0; 24]$ est 9 et il est atteint en $t = 3$.
