L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
La figure ci-dessous est la représentation graphique d'une fonction \(f\) définie sur \(\mathbb{R}\).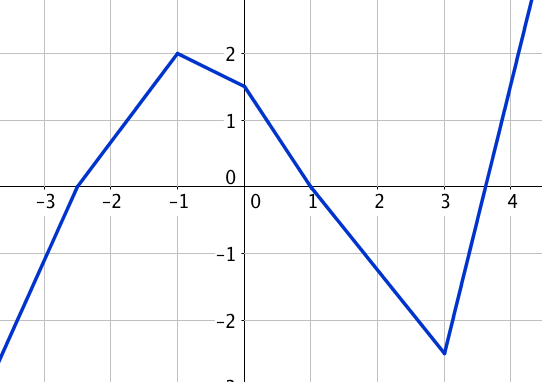 
Cochez la bonne réponse.
La fonction est toujours négative et positive.
La fonction est croissante et décroissante.
La fonction est plutôt globalement décroissante.
Aucune des trois réponses précédentes n’est exacte.
On peut répondre par une phrase ou un tableau.
Chercher les variations de \(f\), c’est chercher les intervalles où la fonction est croissante ou décroissante.
Chercher les variations de \(f\), c’est chercher les intervalles où la fonction est croissante ou décroissante.
Il faut ici préciser sur quels intervalles la fonction est croissante ou décroissante. C’est la raison pour laquelle on préfère en général faire un tableau qui résume tout cela.
Question 2
Une seule des 4 affirmations suivantes est correcte.
Cochez la bonne réponse.
\(f\left( -\dfrac{19}{12} \right) > f\left( -\dfrac{5}{3} \right)\)
\(f\left( -\dfrac{1}{2} \right) < f\left( \dfrac{1}{2} \right)\)
\(f(0) < f(1)\)
Pour tout réel \(x\), \(f(x) \geq -2,5\)
Il faut ici se rappeler de la vraie définition d’une fonction croissante ou décroissante. Besoin d’un rappel ? Allez voir la vidéo dans les prérequis.
Il faut ici comparer deux fractions. Seule issue : les réduire…
...au même dénominateur
Il faut ici comparer deux fractions. Seule issue : les réduire…
...au même dénominateur
On ne peut pas répondre à cette question sans connaître la définition du cours d’une fonction croissante ou décroissante. Vous allez utiliser ces notions jusqu’au bac. Autant les apprendre une bonne fois pour toutes.
Question 3
On considère une fonction \(f\) définie sur l'intervalle $[-7 ; 10]$ telle que \(f(0) = 2\) .
Le tableau de variations de la fonction \(f\) est le suivant :
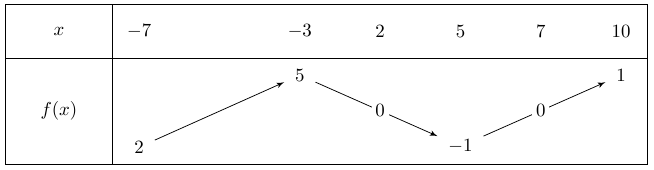
Peut-on comparer les images de $-4$ et de $8$ ?
En faisant la même chose avec \(f(8)\) vous pouvez conclure.
Oui, $-4$ est plus petit que $8$ donc \(f(-4) < f(8)\)
Non, on sait juste que ces deux images sont positives.
Oui, \(f(-4) > f(8)\).
Aucune des trois réponses précédentes n’est exacte.
Essayez d’encadrer l’image de \(f(-4)\). Cela signifie trouver la plus petite et la plus grande valeur possible.
Vous devez savoir répondre avec des courbes ou avec des tableaux de variations. Si vous avez du mal à visualiser ce qui se passe, tracez une courbe au brouillon qui coïncide avec les variations de \(f\). Vous comprendrez alors pourquoi \(f(-4) > f(8)\).
Question 4
Peut-on résoudre avec les données de l'énoncé l'inéquation \(f(x)\ \geq 2\)
Si oui, donner l'ensemble des solutions.
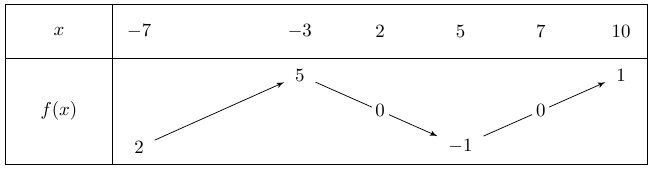
Oui et \(S= \varnothing\).
Oui et \(S = [-7 ; -2]\) ou \(S = [-7 ; -1]\).
Non.
Aucune des trois réponses précédentes n’est exacte.
Essayez d’imaginer que ce tableau est associé à une courbe de température.
On se demande pour quelle valeur de \(x\), la température serait supérieure ou égale à 2.
On se demande pour quelle valeur de \(x\), la température serait supérieure ou égale à 2.
Attention !! Pas de valeurs approchées pour les solutions. On a bien l’intuition que lorsque \(x\) se situe entre -3 et 2, la valeur de \(f(x)\) va valoir 2 puisqu’elle prend toutes les valeurs comprises entre 0 et 5. Mais comment savoir pour quelle valeur précise de \(x\) ? Impossible ici donc on ne peut pas résoudre cette inéquation avec les seules données de l’énoncé.