Fonctions croissantes, décroissantes

Fonctions croissantes, décroissantes

Fonctions croissantes, décroissantes

Définitions.

Soit $f$ une fonction définie sur un intervalle $I$.

a) Pour tous réels $a$ et $b$ appartenant à $I$ tels que $a \leq b$,

si $f(a) \leq f(b)$ alors la fonction est croissante.

b) Pour tous réels $a$ et $b$ appartenant à $I$ tels que $a \leq b$,

si $f(a) \geq f(b)$ alors la fonction est décroissante.

Exemples

Soient deux fonctions $f$ et $g$ représentant l'évolution de la température en fonction du temps.

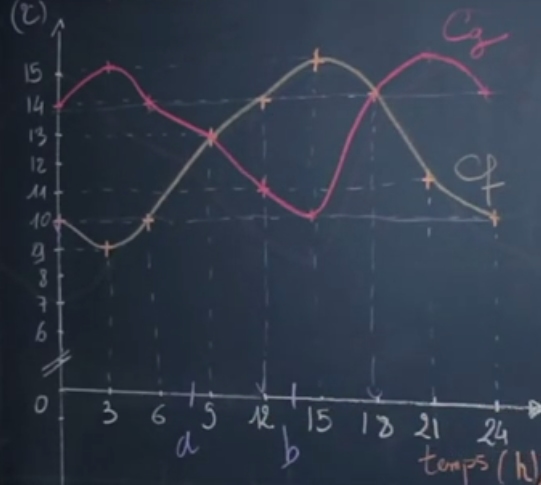
Considérons la fonction $f$ sur $[3; 15]$.

$f$ est croissante sur cet intervalle, la température augmente entre 3h et 15h. 

Considérons de même la fonction $g$ sur $[3; 15]$.

$g$ est décroissante sur cet intervalle, la température diminue entre 3h et 15h.