L'énoncé
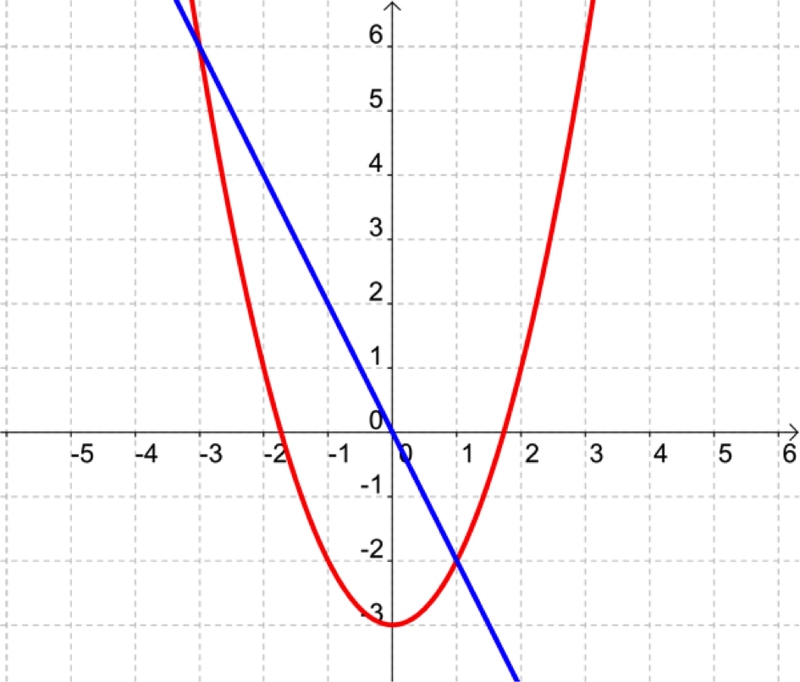
On considère les fonctions \(f\) et \(g\) définies sur \(\mathbb{R}\) :
\(f(x) = x^2 - 3\)
\(g(x) = -2x\)
Ces fonctions ont été représentées ci-dessous.
Tu as obtenu le score de
Question 1
Quelle est la nature de \(g\) ?
\(g\) est une fonction linéaire et son coefficient directeur vaut \(-2\).
\(g\) est une fonction linéaire et son coefficient directeur vaut \(-2x\).
\(g\) n'est pas une fonction linéaire.
Aucune des réponses précédentes n’est exacte.
Connaissez-vous la définition d’une fonction linéaire ?
Faites bien attention au coefficient directeur. C'est une constante !
Question 2
La fonction \(f\) est-elle inspirée d'une fonction de référence ?
Non.
Oui de la fonction inverse.
Oui de la fonction carré.
Aucune des réponses précédentes n’est exacte.
Normalement, c'est assez évident...
Ne vous laissez pas impressionner par la constante -3. Ce nombre a juste pour effet de décaler la courbe de trois unités vers le bas.
Question 3
Résolvez graphiquement : \(f(x) = 1\).
\(S=\{-2;2\}\)
\(S=[-2;2]\)
\(S=]-2;2[\)
Aucune des réponses précédentes n’est exacte.
Il s'agit d'une recherche d'antécédent.
Des antécédents de 1 bien sûr (s’il y en a ) !
Question 4
Résolvez à présent par le calcul \(f(x)=1\).
\(S = [-2 ;2]\)
\(S =\{-2 ;2\}\)
\(S=]-2;2[\)
Aucune des réponses précédentes n’est exacte.
Écrivez l’équation proposée.
Regroupez tous les termes dans le membre de gauche de l’équation.
Essayez de faire apparaitre une égalité remarquable.
\(x^2-4 = 0\) se factorise facilement.
Question 5
Résolvez graphiquement \(f(x) < 1\).
\(S=\{-2;2\}\)
\(S=[-2;2]\)
\(S=]-2;2[\)
Aucune des réponses précédentes n’est exacte.
Il s'agit d'une inéquation. Attention au signe !
Cherchez les valeurs de \(x\) pour lesquelles la fonction prend des valeurs strictement inférieures à 1.
Question 6
Résolvez graphiquement \(g(x)>4\).
\(S = [-\infty ; -2[\)
\(S = ]-\infty ; -2[\)
\(S = ]-2; +\infty [\)
Aucune des réponses précédentes n’est exacte.
Avez-vous repéré la portion de la droite dont les ordonnées sont supérieures à 4 ?
Question 7
Résolvez graphiquement l'équation \(f(x) = g(x)\).
\(S=\{-3 ;1\}\)
\(S=\{-3 ;0\}\)
\(S=\{0 ;1\}\)
Aucune des réponses précédentes n’est exacte.
Lorsque \(f(x) = g(x)\), cela signifie que \(f\) et \(g\) ont la même image du nombre \(x\).
Avez-vous repéré les points de la courbe où cela se produit ?
Cherchez à présent les valeurs de \(x\) correspondantes.
Question 8
Résolvez graphiquement \(f(x) < g(x)\).
\(S = [-3 ;1]\)
\(S = ]-3 ;1[\)
\(S = [-3 ;0]\)
Aucune des réponses précédentes n’est exacte.
Repérez la portion de courbe où la courbe \(C_f\) est en dessous de la droite \(C_g\).
Cherchez les valeurs de \(x\) correspondantes.
Question 9
On souhaite résoudre \(f(x) = g(x)\) par le calcul.
Écrivez cette équation et développez ensuite \((x-1)(x+3)\). Que remarque-t-on ?
\((x-1)(x+3) = x^2+2x-3\)
\((x-1)(x+3) = x^2-3\)
\((x-1)(x+3) = 2x-3\)
Aucune des réponses précédentes n’est exacte.
Rien d’autre à faire que de développer.
Et de remarquer que c’est une expression que l’on vient de rencontrer…
Question 10
Résolvez à présent l'équation \((x-1)(x+3) = 0\) pour trouver les solutions de \(f(x) = g(x)\).
\(S=\{-3 ;-1\}\)
\(S=\{1 ;3\}\)
\(S=\{3 ;-1\}\)
Aucune des réponses précédentes n’est exacte.
C’est une équation produit.
Ne développez surtout pas.
\((x-1)(x+3) = 0\) équivaut à ce \((x-1) = 0\) ou \((x+3) =0\).
