L'énoncé
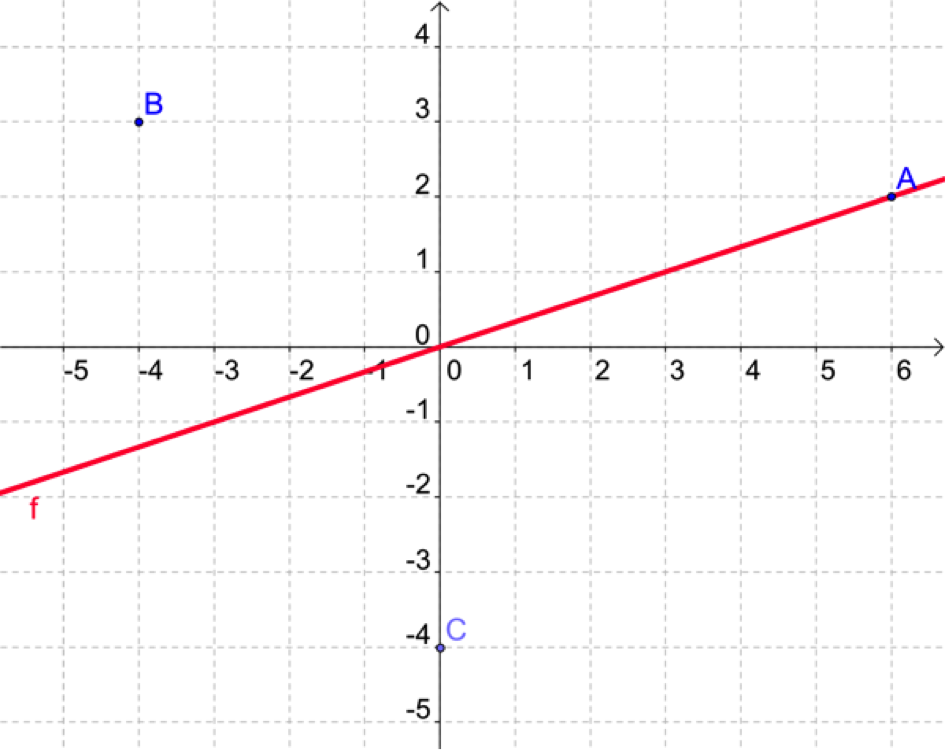
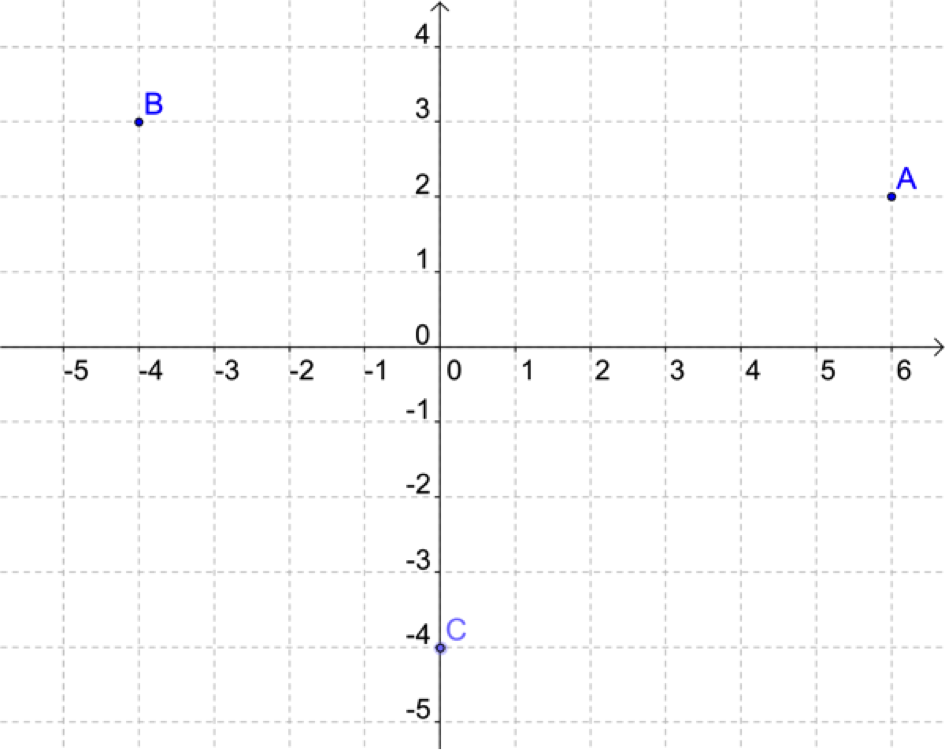
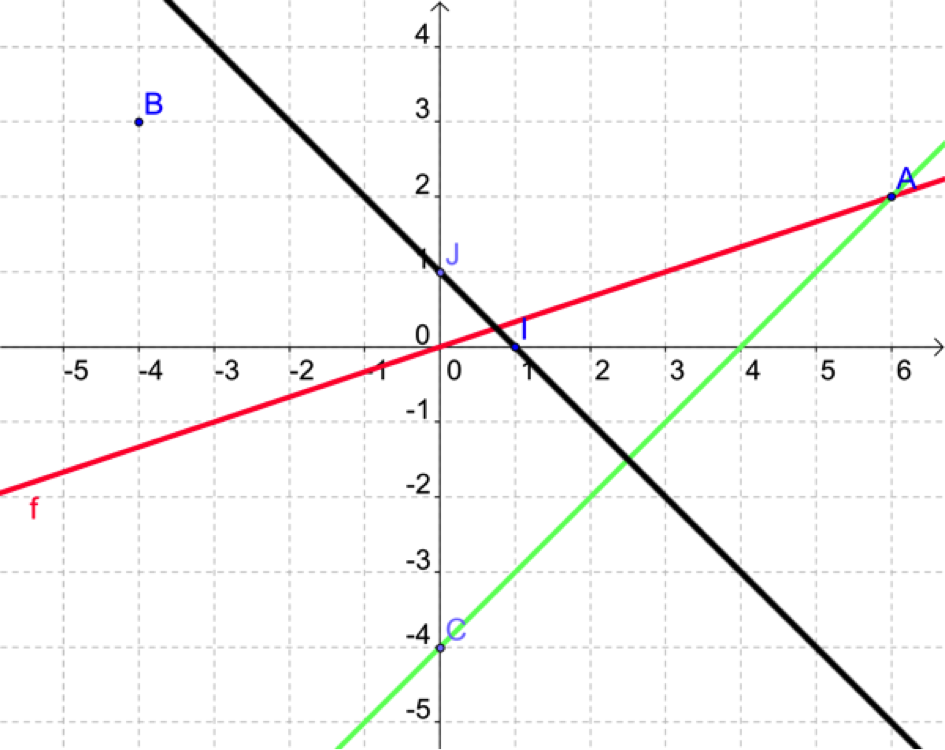
On considère les points \(A(6 ;2), B(-4 ; 3)\) et \(C(0 ;-4)\) dans un repère orthonormé \((O ;I ;J).\)
Vous pouvez faire votre propre figure ou imprimer l’image de la première question. Nous vous suggérons de la compléter au fur et à mesure de l’exercice.
Tu as obtenu le score de
Question 1
Déterminez la fonction linéaire \(f\) telle que \(C_f\), sa représentation graphique, passe par \(A (6 ;2).\)
\(f(x) = 3x\)
\(f(x) = 0,3x\)
\(f(x) = \dfrac{1}{3} \times x\)
Aucune des réponses précédentes n’est exacte.
\(f\) est linéaire donc de la forme : \(f(x) = ax.\)
Si \(C_f\) passe par \(A\), alors \(f(…) =\) ?
Ainsi on a : \(6a = 2\). Vous n'avez plus qu’à trouver \(a\) pour conclure.
Question 2
Elle est croissante.
Elle est constante.
Elle est décroissante.
Aucune des réponses précédentes n’est exacte.
Savez-vous ce qu’est une fonction croissante ? Allez voir la vidéo dans les prérequis.
Pour les fonctions linéaires, il suffit de trouver le signe du coefficient directeur.
Ici, \(\dfrac{1}{3}\) est un nombre positif donc \(f\) est ?
Question 3
On note à présent \(g\) la fonction affine telle que \(C_g\) passe par \(A\) et \(C.\)
Notons \(g(x) = mx+p.\)
Le nombre \(m\) est le coefficient directeur. Quelle est sa valeur ?
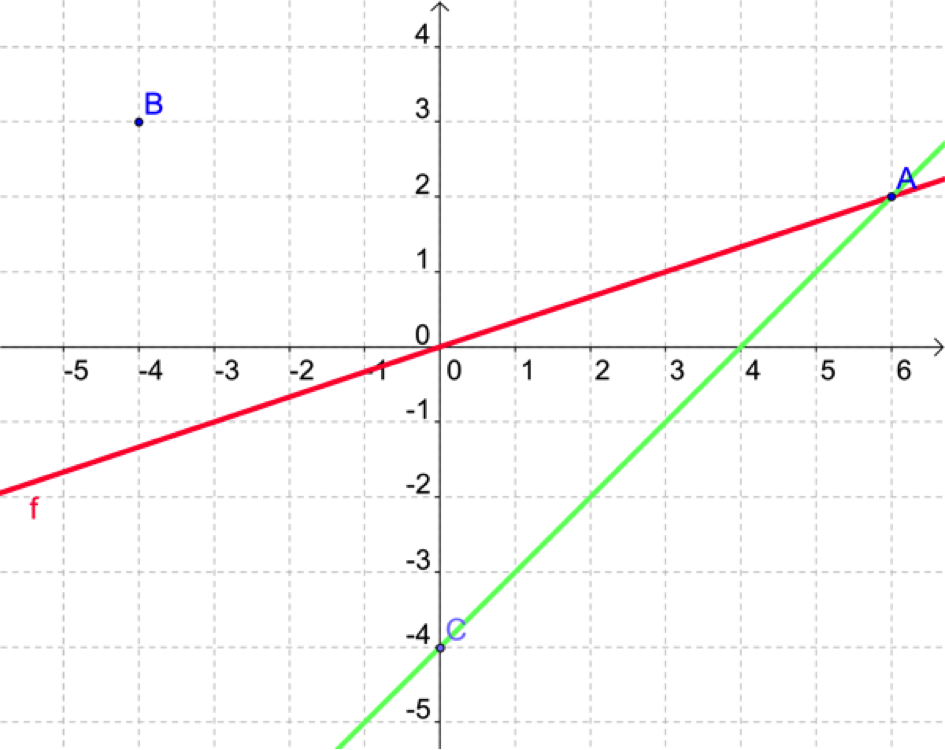
\(m=1\)
\(m=-1\)
\(m= \dfrac{1}{2}\)
Aucune des réponses précédentes n’est exacte.
Il y a une formule dans votre cours pour calculer un coefficient directeur. La connaissez-vous ? Sinon regardez la vidéo dans les prérequis.
Vous pouvez aussi utiliser une lecture graphique si vous savez faire.
Question 4
On a donc \(g(x) = 1x+p\) que l'on écrira \(g(x) = x+p.\)
Calculez ou lisez sur le graphique la valeur de \(p\).

\(p=0\)
\(p=4\)
\(p=-4\)
Aucune des réponses précédentes n’est exacte.
Graphiquement c’est évident : le nombre \(p\) est par définition l’ordonnée à l’origine.
Le point \(C\) a justement un abscisse nulle donc son ordonnée peut être utile…
Question 5
On a donc \(g(x)= x-4.\)
Notons \(D\) le point de \(C_g\) d'abscisse \(101\), volontairement hors cadre.
Quelles sont les coordonnées de \(D\) ?
\(D(101 ; 101)\)
\(D(101 ; 105)\)
\(D(101 ; 97)\)
Aucune des réponses précédentes n’est exacte.
On cherche l’image de \(101\) par \(g.\)
Il suffit de remplacer \(x\) par... ?
Question 6
Notons à présent \(h\) la fonction telle que \(C_h\) passe par \(I\) et \(J.\)
Tracez \(C_h\) sur votre figure.
Donnez l'expression de \(h(x)\) par une simple lecture graphique.
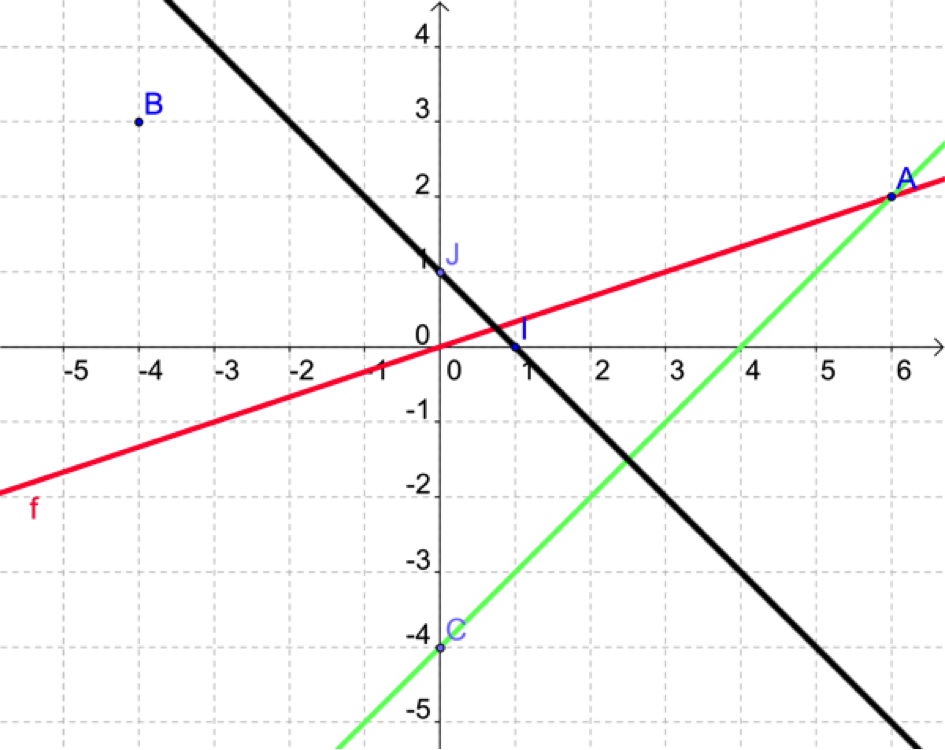
\(h(x) = x+1\)
\(h(x) = -x+1\)
\(h(x) = -x-1\)
Aucune des réponses précédentes n’est exacte.
Pour le coefficient directeur, connaissez-vous une méthode graphique ? Sinon regardez la vidéo dans les prérequis.
L’ordonnée à l’origine se trouve en s’intéressant au point \(J.\)
Question 7
On sait d'après les questions précédentes que :
\(g(x) = x-4\) et que \( h(x) = -x+1.\)
Notons \(H(x_H ; y_H)\) le point d'intersection de \(C_g\) et de \(C_h.\) Placez \(H\) sur votre figure.
Quelle équation doit-on résoudre pour trouver les coordonnées de \(H\) ?
\(g(H) = H\)
\(g(x) = h(x)\)
\(x=y\)
Aucune des réponses précédentes n’est exacte.
Puisque \(H\) appartient à \(C_g\) et à \(C_h\), ses coordonnées vérifient les deux équations de ces deux courbes.
\(g(x_H) = x_H -4\)
\(h(x_H) = - x_H +1\)
Question 8
On doit donc résoudre : \(x-4 = -x+1.\)
Quelle est la solution de cette équation ?
\(x= 2\)
\(x =-5\)
\(x=2,5\)
Aucune des réponses précédentes n’est exacte.
C’est une équation du premier degré.
Regroupez les termes en \(x.\)
Question 9
Cherchez à présent les coordonnées du point \(H(x_H ; y_H)\) sachant qu'on a trouvé \(x_H =2,5.\)
On rappelle : \(h(x) = -x+1\)
\(H(2,5 ; -1,5)\)
\(H(2,5 ; -1)\)
\(H(2,5 ; -1,3)\)
Aucune des réponses précédentes n’est exacte.
Il suffit de remplacer \(x\) dans l’expression de \(g(x)\) ou de \(h(x).\)
Question 10
Vous pouvez vérifier sur le graphique les coordonnées de \(H.\)
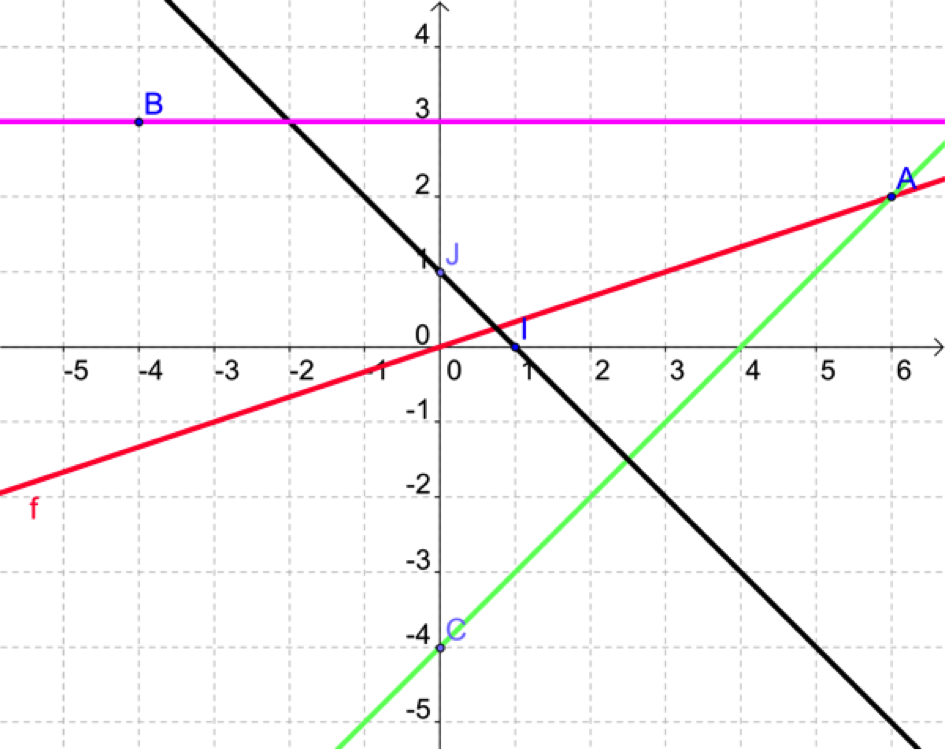
On trace à présent la droite passant par \(B\) et parallèle à l'axe des abscisses.
Cette droite est la représentation graphique dune fonction notée \(b(x).\)
Quelle est son expression ?
\(b(x)=x\)
\(b(x)=3\)
\(x=3\)
Aucune des réponses précédentes n’est exacte.
Est-ce une fonction affine, linéaire, ni l’une ni l’autre ?
Pensez au coefficient directeur de la droite.