Fiche de cours
Fonctions linéaires et affines
Définition
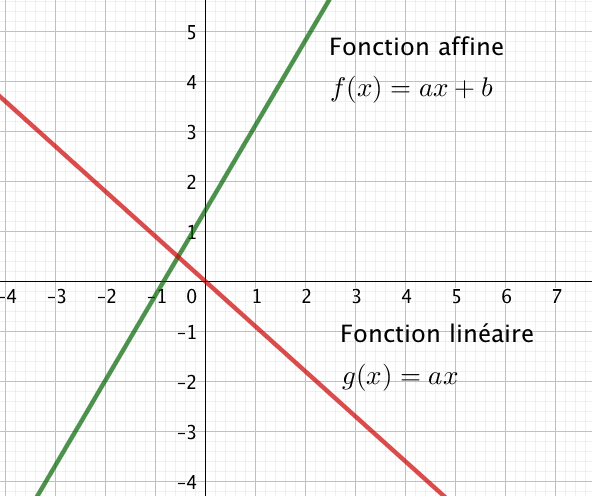
Une fonction affine est une fonction de la forme : $f(x) = ax + b$
Le nombre $a$ est le coefficient directeur de la droite, c'est à dire celui qui donne la pente de la droite, $x$ est la variable.
Le nombre $b$ l'ordonnée à l'origine, c'est à dire la valeur de la fonction lorsque $x = 0$.
Une fonction linéaire est une fonction affine particulière où $b = 0$ :
$g(x) = ax$, il s'agit d'une droite passant par l'origine.
Variations de fonctions affines
Si le coefficient directeur est strictement positif, alors la fonction $f$ est croissante sur $\mathbb{R}$.
Si le coefficient directeur est strictement négatif, alors la fonction $f$ est décroissante sur $\mathbb{R}$.
Si le coefficient directeur est nul, $f$ est constante sur $\mathbb{R}$ dont la représentation graphique est une droite parallèle à l'axe des abscisses.
Signe de $f(x)$
On regarde pour quelles valeu