L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
La figure ci-dessous représente un carré $ABCD$ et un rectangle $DEFG$.
$E$ est un point du segment $[AD]$.
$C$ est un point du segment $[DG]$.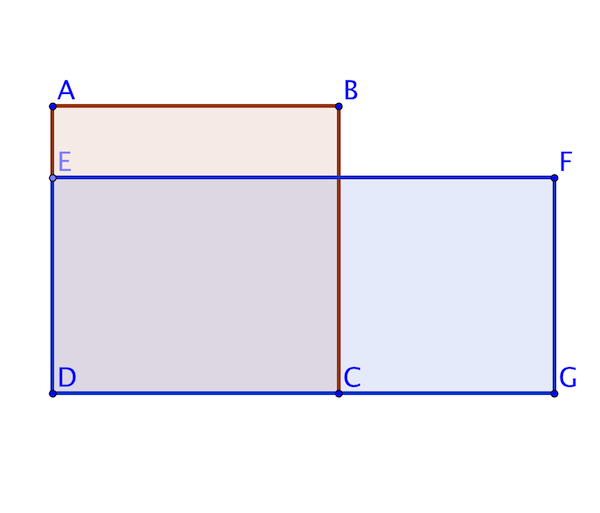
Sur cette figure, la longueur $AB$ peut varier mais on a toujours :
$AE = 15$ cm et $CG = 25$ cm.
Tu as obtenu le score de
Question 1
Dans cette question, on suppose que $AB = 40$ cm.
À combien est égale l'aire du carré $ABCD$ ?
$160 $\(cm^2\)
$1 600$ \(cm^2\)
$16$ \(cm^2\)
$80$ \(cm^2\)
L’aire d’un carré de côté \(c\) est donnée par la formule : \(Aire = c^2\)
Et ce côté est égal à $40$ cm.
Question 2
Dans cette question, on suppose encore que $AB = 40$ cm.
À combien est égale l'aire du rectangle $DEFG$ ?
$1625$ \(cm^2\)
$90$ \(cm^2\)
$225$ \(cm^2\)
$625$ \(cm^2\)
L’aire d’un rectangle de Longueur \(L\) et de largeur \(l\) est donnée par la formule : \(Aire = L \times l\)
La longueur de \(DEFG\) est égale à \(DC + CG\) ...
Et la largeur de \(DEFG\) est égale à \(AD – AE\).
Question 3
Dans la suite du problème, $AB$ n'est plus égal à $40$ cm ! Justement, on cherche à déterminer la longueur $AB$ notée \(x\) de sorte que l'aire du carré $ABCD$ soit égale à l'aire du rectangle $DEFG$.
Quelle équation devra-t-on résoudre pour déterminer $AB$ ?
\(x^2=(x+15)(x-25)\)
\(x^2=(x-15)(x+25)\)
\(x^2=(x-15)(x-25)\)
\(x^2=(x+15)(x+25)\)
Si le côté du carré \(ABCD\) est égal à \(x\), alors son aire est égale à \(x^2\).
Et la largeur de \(DEFG\) est égale à \(AD – AE\).
Or \(AD = BC = x\) et \(AE = 15 \ cm\).
La longueur de \(DEFG\) est égale à \(DC + CG\), or :
\(DC = AB = x\) et \(CG = 25 \ cm\)
Question 4
C'est parti pour la résolution de cette équation : \(x^2=(x-15)(x+25)\)
Quelle est l'étape suivante de la résolution ?
\(x^2=x^2-25x+15x-375\)
\(x^2=x^2+25x+15x+375\)
\(x^2=x-15+x+25\)
\(x^2=x^2+25x-15x-375\)
On se souvient, double distributivité : \((a+b)(c+d)=ac+ad+bc+bd\)
Ce qui donne avec les signes de notre équation : \((a-b)(c+d)=ac+ad-bc-bd\)
Question 5
On en est à : \( x^2=x^2+25x-15x-375\)
Quelle est l'étape suivante de la résolution ?
\(2x^2=10x-375\)
\(0=10x-375\)
\(0=50x-375\)
\(2x^2=15x-375\)
Sautez sur l’opportunité : il faut bien sûr soustraire \(x^2\) dans chaque membre.
Et il suffit maintenant de diviser par $10$ dans chaque membre pour finir d’isoler \(x\).
Question 6
On a : \( 0=10x-375\)
Quelle est la solution de l'équation ? Et par conséquent, à combien doit être égal $AB$ pour que le carré $ABCD$ et le rectangle $EFGH$ aient la même aire ?
$385$
$3,75$
$365$
$37,5$
Étape suivante de la résolution (à faire de tête) : \( 375=10x\)
Et il suffit maintenant de diviser par $10$ dans chaque membre pour finir d’isoler \(x\).
Conclusion : les deux aires seront égales lorsque \(x \) prend la valeur $37,5$ cm.
