Fiche de cours
Suites géométriques
1) Définition
Une suite géométrique est une suite pour laquelle chaque terme permet de déduire le suivant en étant multiplié par une constante $q$, la raison.
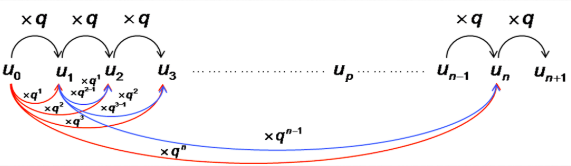
Une suite géométrique est ainsi définie par
$\left \{ \begin{array}{l} u_{n + 1} = u_n \times q \\ u_0 \\ \end{array} \right.$ où $q$ est la raison ($q \in \mathbb{R}$) et $u_0$ est le premier terme de la suite.
Considérons une suite géométrique de raison $2$ de premier terme 5 qui s'écrit alors :
$\left \{ \begin{array}{l} u_{n + 1} = u_n \times 2 \\ u_0=5 \\ \end{array} \right.$
Les premiers termes de la suite sont donc :
$u_1 = u_0 \times 2 = 5 \times 2 = 10$ et
$u_2 = u_1 \times 2 = 10 \times 2 = 20$.
Propriété : expression de $u_n$ en fonction de $n$.
Néanmoins la définition d'une suite géométrique nécessite pour calculer un terme de la suite d'avoir au pr&eac
