Fiche de cours
Suites arithmétiques
Définition
Une suite arithmétique est une suite pour laquelle chaque terme permet de déduire le suivant en lui ajoutant le même nombre : la raison $r$.
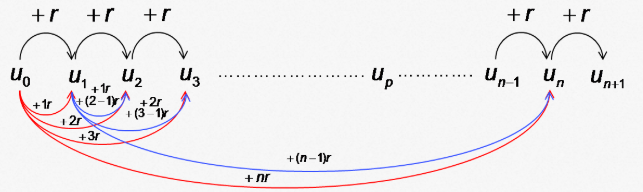
Pour définir une suite arithmétique $(u_n)_{(n \in \mathbb{N})}$, il faut un premier terme, $u_0$ généralement, et la raison $r$ ($r \in \mathbb{R}$).
On écrit alors : $\left \{ \begin{array}{l} u_{n + 1} = u_n + r \\ u_0 \\ \end{array} \right.$
Exemple :
Considérons la suite $\left \{ \begin{array}{l} u_{n + 1} = u_n - 7 \\ u_0 = 17 \\ \end{array} \right.$.
On obtient donc $u_1 = 17 - 7 = 10$ et $u_2 = 10 - 7 = 3$.
Cette définition par récurrence ne permet cependant pas de trouver directement n'importe quel terme de la suite : il faut avoir calculé tous les termes précédents.
Il existe néanmoins une formule générale, dite explicite, qui permet de calculer n'importe quel terme de la suite.
