Fiche de cours
Loi binomiale - Schéma
Considérons la loi binomiale de paramètres $n = 3$ et $p = \dfrac{1}{6}$.
Cela signifie que l'on répète trois fois l'expérience et que la probabilité du succès est $\dfrac{1}{6}$.
Un arbre pondéré est utile pour représenter la loi binomiale.
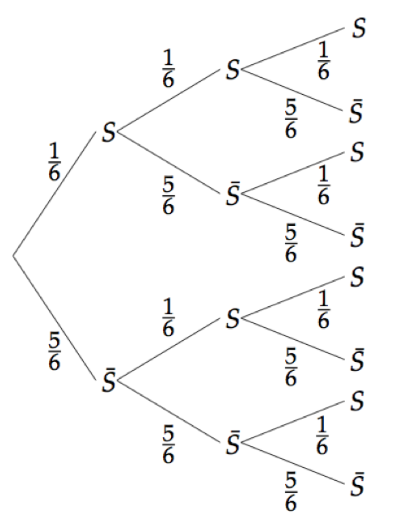
La variable aléatoire associée à la loi binomiale est $X$. Cette dernière permet de compter le nombre de succès.
En considérant le premier chemin par exemple, on rencontre trois fois la lettre $S$ : ainsi, $X = 3$.
Ainsi, $X$ est compris entre 0 et 3.
L'arbre permet de calculer des probabilités.
Exemple
Calculons $P(X = 3)$.
En regardant l'arbre, on remarque que cet événement n'a lieu qu'une fois.
Pour obtenir la probabilité associée, il faut alors multiplier entre elles les probabilités inscrites sur les branches parcourues;
$P(X = 3) = \dfrac{1}{6} \times \dfrac{1}{6} \times \dfrac{1}{6} = \dfrac{1}{216}$.
