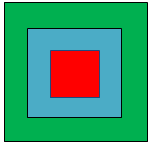
Dans un jeu de fléchettes, la cible est constituée de carrés de côtés respectifs $5$, $15$ et $25$ cm.
Un joueur atteint toujours la cible et on admet que la probabilité qu'il atteigne une zone de cette cible est proportionnelle à l'aire de cette zone.
Lorsqu'il atteint la zone rouge, il gagne $10$ euros, lorsqu'il atteint la zone bleue, il gagne $6$ euros. En revanche si la fléchette atteint la zone verte, il perd $4$ euros.
On appelle $X$ la variable aléatoire qui donne le gain algébrique du joueur.
1) Déterminer la loi de probabilité de $X$.
2) Calculer $E(X)$ et commenter cette valeur.
1) Les probabilités des différentes zones sont proportionnelles à leur surface, il faut donc calculer les surfaces de ces différentes zones (en $cm^2$).
La surface totale de la cible est $25^2 = 625$.
La surface de la zone rouge est $5^2 = 25$.
La surface de la zone bleue est $15^2 - 25 = 200$.
La surface de la zone verte est $25^2 - (200+25) = 400$.
Maintenant, on peut déterminer les probabilités.
Si la zone rouge est atteinte, le joueur gagne $10$ euros, donc $X$ prend la valeur $10$ avec une probabilité de $\dfrac{25}{625} = 0.04$. On a donc $p(X=10) = 0.04$.
Si la zone bleue est atteinte, le joueur gagne $6$ euros, donc $X$ prend la valeur $6$ avec une probabilité de $\dfrac{200}{625}= 0.32$. On a donc $p(X=6) = 0.32$.
Si la zone verte est atteinte, le joueur perd $4$ euros, donc $X$ prend la valeur $-4$ avec une probabilité de $\dfrac{400}{625} = 0.64$. On a donc $p(X=-4) = 0.64$.
2) L’espérance vaut $E(X) = -4 \times 0.64 + 6 \times 0.32 + 10 \times 0.04 = -0.24$.
C’est la valeur que prend la variable aléatoire $X$ en moyenne. Le joueur perdra donc en moyenne environ $24$ centimes. Le jeu est donc défavorable au joueur.
