L'énoncé
On dispose de deux urnes différentes A et B :
• L’urne A contient 4 boules rouges, 6 jaunes, et 5 vertes.
• L’urne B contient 4 boules rouges et 6 vertes.
Le jeu proposé est le suivant :
On lance un dé bien équilibré : si le résultat est 1 ou 2, on tire une boule dans l’urne A. Sinon, on tire une boule dans l’urne B.
Le joueur gagne 10 euros si la boule tirée est rouge, 5 euros si elle est jaune et perd 3 euros si elle est verte.
On note \(X\) le gain du joueur à l’issue de ce jeu.
Question 1
Donner les valeurs possibles de \(X\).
Les valeurs de \(X\) sont \(\{-3 ; 5 ; 10 \}\).
Aucun calcul n’est encore demandé ici.
Question 2
Construire un arbre pondéré décrivant la situation exposée dans l'énoncé.
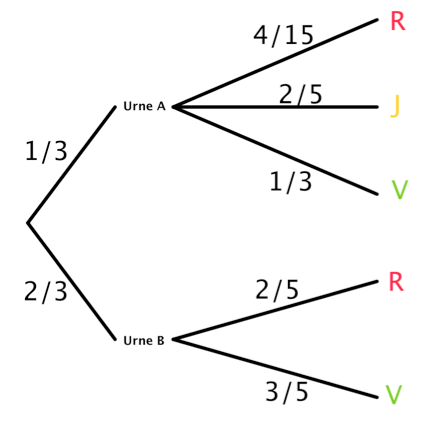
Probabilités pour le choix de l'urne :
Probabilité d'obtenir l'urne A = \(\dfrac{2}{6}=\dfrac{1}{3}\)
Probabilité d'obtenir l'urne B = \(\dfrac{2}{3}\)
Dans l'urne A :
\(p(R) =\dfrac{4}{15}\) (4 boules rouges sur un total de 15 boules)
\(p(J) =\dfrac{6}{15}=\dfrac{2}{5}\) (6 boules jaunes sur un total de 15 boules)
\(p(V) = \dfrac{5}{15}=\dfrac{1}{3}\) (5 boules vertes sur un total de 15 boules)
Dans l'urne B :
\(p(R) = \dfrac{4}{10} =\dfrac{2}{5} \) (4 boules rouges sur un total de 10 boules)
\(p(V) = \dfrac{6}{10}=\dfrac{3}{5}\) (6 boules vertes sur un total de 10 boules)
A partir de l’urne A, énoncer les possibilités pour la boule tirée : elle est rouge, jaune ou verte : calculer alors les 3 probabilités correspondantes.
Question 3
Quelle est la probabilité de gagner 10 euros ?
Gagner 10 euros, c'est avoir tiré une boule rouge : soit la boule est rouge et vient de l'urne A, soit elle est rouge et vient de l'urne B.
La probabilité d'obtenir une boule rouge venant de l'urne A est : \(\dfrac{1}{3}\times \dfrac{4}{15} = \dfrac{4}{45} \)
La probabilité d'obtenir une boule rouge venant de l'urne B est : \(\dfrac{2}{3}\times \dfrac{2}{5} = \dfrac{4}{15} \)
La probabilité de gagner 10 euros est alors :
\(p(X =10)= \dfrac{4}{45} + \dfrac{4}{15} = \dfrac{16}{45} \)
Ensuite, on utilise l’arbre et on repère les chemins qui mènent à une boule rouge.
La probabilité d’obtenir une boule rouge venant de l’urne A est : \(\large\frac{1}{3}\times \frac{4}{15} \) (et oui, c’est bien un produit).
Même technique avec le produit des probabilités pour trouver la probabilité d’obtenir une boule rouge venant de l’urne B.
Question 4
Déterminer la loi de probabilité de \(X\).
On peut compléter l'arbre avec les valeurs de \(X\) :
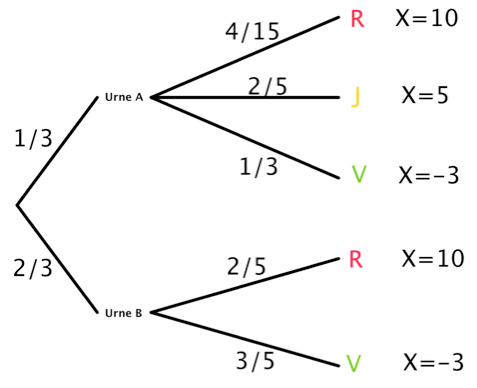
Probabilité d'avoir une boule jaune \((X=5)\) :
Le seul moyen d'avoir une boule jaune est d'obtenir d'abord l'urne A.
La probabilité d'obtenir une boule jaune venant de l'urne A est donc : \(\dfrac{1}{3} \times \dfrac{2}{5} = \dfrac{2}{15}\)
Probabilité d'avoir une boule verte \((X=-3)\) :
La probabilité d'obtenir une boule verte venant de l'urne A est : \(\dfrac{1}{3} \times \dfrac{1}{3} = \dfrac{1}{9}\)
La probabilité d'obtenir une boule verte venant de l'urne B est : \(\dfrac{2}{3} \times \dfrac{3}{5} = \dfrac{2}{5}\)
La probabilité d'avoir une boule verte est alors : \(\dfrac{1}{9} + \dfrac{2}{5} = \dfrac{23}{45}\).
C'est \(p(X =-3)\) !
La loi de probabilité de \(X\) est alors :
| Valeurs de \(X\) | \(10\) | \(5\) | \(-3\) |
| \(p(X=x_i)\) | \(\dfrac{16}{45}\) | \(\dfrac{2}{15} \) | \(\dfrac{23}{45}\) |
Utiliser l’arbre pondéré : on peut rajouter au bout de chaque chemin de l’arbre, la valeur du gain correspondant.
Trouver la probabilité d’obtenir une boule jaune : un seul chemin mène à la boule jaune…
Question 5
Quelle est l'espérance de \(X\) ?
\(E(X) = 10 \times \dfrac{16}{45} + 5 \times \dfrac{2}{15} - 3 \times \dfrac{23}{45} \)
\(E(X) = \dfrac{160}{45} + \dfrac{10}{15} - \dfrac{ 69}{45} \)
\(E(X) = \dfrac{121}{45}\)
$E(X)\approx 2,69$
Question 6
Interpréter d'une phrase le résultat de la question 5.
Lorsque l'on joue un grand nombre de fois à ce jeu, on peut espérer gagner en moyenne \(\dfrac{121}{45}\) soit $2,69$ euros environ.
Le plus significatif est le signe : en moyenne, le gain est positif pour ce jeu !
