L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
On a relevé ci-dessous le prix d'un même article dans différents magasins d'une grande ville :
| Prix (en euros) | 11 | 12 | 13 | 14 | 15 | 16 |
| Nombre de magasins | 16 | 20 | 40 | 69 | 73 | 31 |
L’étendue de cette série est 5.
L’étendue de cette série est 16.
La médiane est 125.
La médiane est 14.
Étendue = \(V_{max} - V_{min}\)
Trouver l’effectif total : est-il pair ou impair ?
L’effectif total est 249 : utiliser la règle de calcul de la médiane.
Il faut prendre la valeur de rang 125.
L’étendue est 16 - 11 = 5 euros. (Proposition 1 vraie et 2 fausse.)
L’effectif total est 249 (impair) : on a \(\frac{(249+1)}{2}=125\). Il faut alors prendre la valeur de rang 125.
En additionnant les effectifs, on obtient que 16 + 20 + 40 = 76 (nombre de valeurs inférieures à 13) et 16 + 20 + 40 + 69 = 145 (nombre de valeurs sont inférieures 14).
La valeur de rang 125 est 14 Donc \(M_e=14\). (Proposition 4 vraie.)
On peut directement dresser le tableau contenant les effectifs cumulés croissants : cela est utile pour les calculs de la médiane et des quartiles.
Ici, c’est :
Effectifs cumulés croissants
| Prix (en euros) | 11 | 12 | 13 |
Question 2On a relevé ci-dessous le prix dun même article dans différents magasins dune grande ville :
Le premier quartile est 12 euros. Le premier quartile est 13 euros. Au moins trois quarts des magasins étudiés proposent un prix inférieur à 15 euros. La moitié des magasins proposent un prix compris entre 13 et 15 euros. On commence par l’effectif total… Ici, \(N=249\). Pour trouver les quartiles, on doit trouver \(\dfrac{ N}{4}\) et \(\dfrac{ 3N}{4}\). Ne pas oublier d’arrondir à l’entier juste supérieur. Pour la proposition 3, on doit repérer qu’il est question du troisième quartile. Pour la proposition 4, on doit repérer qu’il est question de l’intervalle interquartile. On a \(N=249\). Pour trouver les quartiles, on calcule \(\frac{N}{4}\) et \(\frac{3N}{4}\), puis on arrondit à l’entier supérieur : \(\frac{N}{4}= 62,25 \) et \(\frac{3N}{4}=186,75\). Le premier quartile est la valeur de rang 63 : \(Q_1=13\) euros. Le troisième quartile est la valeur de rang 187 : \(Q_3=15\) euros. (Propositions 2 et 3 vraies.) L’intervalle interquartile est \([13 ;15] \). (Proposition 4 vraie.) Question 3Une compagnie vendant des forfaits internet étudie le temps d'attente au téléphone de ses clients lorsqu'il contacte l'aide téléphonique :
L’étude porte sur 150 utilisateurs. L’étude porte sur 160 utilisateurs. 90 clients attendent moins de 6 minutes. L’effectif cumulé croissant de la valeur 8 est 50. Le nombre de clients attendant moins de 6 minutes est 20 + 50 +…. Pour trouver l’effectif cumulé croissant de 6, il suffit d’additionner les effectifs correspondants aux valeurs inférieures à 8. L’effectif cumulé croissant de 8 est donc 10 + 50 + 20 + 50. Effectif total = 20 + 50 + 20 + 50 + 20 = 160 clients. (Proposition 2 vraie.) Le nombre de clients attendant moins de 6 minutes est 20 + 50 + 20 = 90. (Proposition 3 vraie.) L’effectif cumulé croissant de 8 est donc 20 + 50 + 20 + 50 = 140. (Proposition 4 fausse.) Question 4On reprend l'étude de la question 4 sur le temps d'attente au téléphone des clients de cette compagnie. Les données sont :
Si on rajoute la ligne donnant les effectifs cumulés croissants, on obtient :
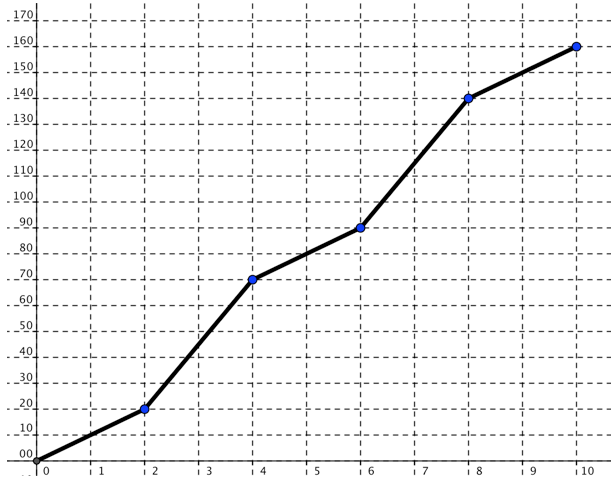
Plus de 50% des clients attendent moins de 6 minutes. Pour construire le diagramme des effectifs cumulés croissants, on place dans un repère les points de coordonnées (2 ; 20) (4 ; 50) (6 ; 20) (8 ; 50) (10 ; 20). Pour construire le diagramme des effectifs cumulés croissants, on place dans un repère les points de coordonnées (2 ; 20) (4 ; 70) (6 ; 90) (8 ; 140) (10 ; 160). Effectifs cumulés croissants : comme son nom l’indique, il suffit de sommer au fur et à mesure les effectifs… Pour la proposition 2, 90 clients attendent moins de 6 minutes : est-ce plus de 50% ? Pour trouver les effectifs cumulés croissants, il suffit d’additionner au fur et à mesure les effectifs. (Proposition 1 vraie.) 90 clients attendent moins de 6 minutes, et ils représentent plus de 50% de la population totale (50% de 160 vaut 80) . (Proposition 2 vraie.) Pour obtenir le diagramme des effectifs cumulés croissants, on prend en abscisse la valeur de droite de la classe (2 pour la première classe qui est [0 ; 2[) puis en ordonnée l’effectif cumulé correspondant : le premier point est donc (2 ; 20). Même technique pour les autres points ! Il faut retenir la méthode pour construire le diagramme des effectifs cumulés croissants : l’abscisse s’obtient en prenant la valeur de droite de la classe (par exemple, dans la classe [2 ; 4[, c’est 4), et l’ordonnée correspondante est l’effectif cumulé croissant associé (ici c’e Question 5On donne le diagramme des effectifs cumulés croissants de la série statistique étudiée aux questions 3 et 4 : La médiane est 80. La moitié des clients attendent moins de 5 minutes. Le premier quartile est environ 2,8. Les trois quarts de clients attendent moins de 7,2 minutes. Pour lire la médiane avec ce type de diagramme, il faut calculer \(\frac{N}{2}\), et placer ce nombre sur l’axe des ordonnées… \(\dfrac{N}{2}=80\). On place 80 sur l’axe des ordonnées et on lit l’abscisse correspondante : c’est la médiane ! Même technique pour la lecture des quartiles, avec \(\dfrac{N}{4}\) ou \(\dfrac{3N}{4}\). \(\dfrac{N}{2}=80\). On place 80 sur l’axe des ordonnées et on lit l’abscisse correspondante : 5 : c’est la médiane ! (Propositions 2 vraie et 1 fausse.) Pour le premier quartile : \(\dfrac{N}{4} =\dfrac{160}{4}=40\). On place 40 sur l’axe des ordonnées et on lit l’abscisse correspondante : c’est 2,8 environ. (Proposition 3 vraie.) Pour le troisième quartile : \(\dfrac{3N}{4} =120\). On place 120 sur l’axe des ordonnées et on lit l’abscisse correspondante : c’est 7,2 environ. (Proposition 4 vraie.) La proposition 4 est fausse : c’est 7 minutes et 15 secondes environ. Tu peux même faire un calcul exact des quartiles : Pour le premier quartile par exemple, on trouve d’abord \(\dfrac{N}{4} = 40 \) On cherche donc l’abscisse \(x\) correspondant à cette ordonnée : le point est sur la droite \((AB)\) o&ugrav |