L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses
Tu as obtenu le score de
Question 1
Le discriminant du trinôme \(2x^2-7x+4\) est :
$0$
$81$
$17$
$-15$
Que valent a, b et c ?
Quelle est la formule pour calculer \(\Delta\) ?
Il ne faut pas hésiter sur ce type de question : \(a = 2\) ; \(b = - 7\) et \(c = 4\) et donc \(\Delta = 17\).
Question 2
Le trinôme \(4x^2-5x+8\) admet :
Aucune racine réelle.
Une racine double.
Deux racines distinctes.
Deux racines opposées.
Que valent a, b et c ? Et \(\Delta\) ?
Quel est le signe de \(\Delta\) ?
\(\Delta < 0\) donc aucune racine !
Pour chercher les racines du trinôme ou résoudre l'équation \(f(x) = 0\) on procède de la même façon : on calcule \(\Delta\) et on conclut sur le nombre de solutions en fonction de son signe.
Question 3
L'équation \(-3x^2-2x+1=0\) admet :
Aucune solution.
Deux solutions de même signe.
Deux solutions : \( \dfrac{1}{3}\) et \(- 1\)
Une solution : 4
Que valent a, b et c ? Et \(\Delta\) ?
Quel est le signe de \(\Delta\) ?
Quelles sont les solutions ?
Ici \(a = - 3 \ ; b = - 2\) et \(c = 1\) et donc \(\Delta = 16\) et l'équation a deux solutions : \(x_1 = \dfrac{1}{3}\) et \(x_2 =-1\)
Les deux solutions pourraient être de même signe. Ce n’est pas le cas ici.
Question 4
Le trinôme \(3x^2-2x-5\) admet pour forme factorisée :
Aucune factorisation possible.
\(3(x+1)\left(x- \dfrac{5}{3}\right)\)
\(3(x-1)\left(x+\dfrac{5}{3}\right)\)
\(3(x-1)^2\)
Que vaut \(\Delta\) ?
Le trinôme admet-il des racines ?
Quelle est alors sa forme factorisée ?
Ici \(\Delta = 64\) et le trinôme a donc deux racines : \(x_1 = \dfrac{5}{3}\) et \(x_2 =-1\). La factorisation du trinôme est alors \(a(x-x_1)(x-x_2)\)
Question 5
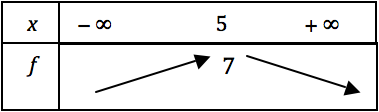
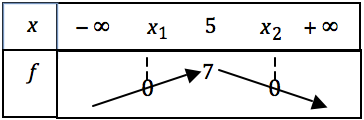
Une fonction polynôme du second degré admet le tableau des variations ci-dessous.
Alors, l'équation \(f(x) = 0 \) a :
Aucune solution.
Une solution unique.
Deux solutions distinctes.
Deux solutions inférieures à $5$.
Quel est le maximum de \(f\) sur \(\mathbb{R}\) ?
\(f\) peut-elle s'annuler ?
\(f\) a pour maximum \(7\) en \(x = 5\) donc la parabole \(C_f\) coupe l'axe des abscisses en deux points et l'équation \(f(x) = 0\) admet alors deux solutions.
Une des solutions est inférieure à $5$ et l'autre supérieure à $5$.
