L'énoncé
On considère la fonction polynôme \(P\) définie sur \(\mathbb{R}\) par : \(P(x) = -2x^2+16x+96\).
On note \(C_P\) sa courbe représentative dans un repère du plan.
Question 1
Résoudre sur \(\mathbb{R}\) l'équation \(P(x) = 0\).
\(P\) est un trinôme du second degré avec \(a = - 2, b = 16\) et \(c = 96\).
Son discriminant \(\Delta\) vaut : \(\Delta = 16^2 - 4\times (-2) \times(96)\)
Donc \(\Delta = 1024\)
\(\Delta > 0\) donc l'équation \(P(x) = 0\) admet deux solutions distinctes :
\(x_1 = \dfrac{-16-32}{-4} =12\) et \(x_2 = \dfrac{-16+32}{-4}= -4\)
L'ensemble solution de \(P(x) = 0\) est \(S = \{-4 ; 12\}\).
Que vaut \(\Delta\) ?
Question 2
Déterminer la forme factorisée de \(P\) sur \(\mathbb{R}\).
\(P\) admet deux racines qui sont \(12\) et \(-4\) ; la forme factorisée de \(P(x)\) est alors :
pour tout réel \(x\), \(P(x) = - 2(x+4)(x-12)\)
Quelle formule utiliser ?
Question 3
Résoudre \(P(x) \geq 0\) en utilisant la forme factorisée de \(P\).
Pour tout réel \(x\), \(P(x)=-2(x-12)(x+4)\) et
\(P(x) = 0 \Leftrightarrow x = 12\) ou \(x = - 4\)
On peut donc dresser le tableau de signes suivant :
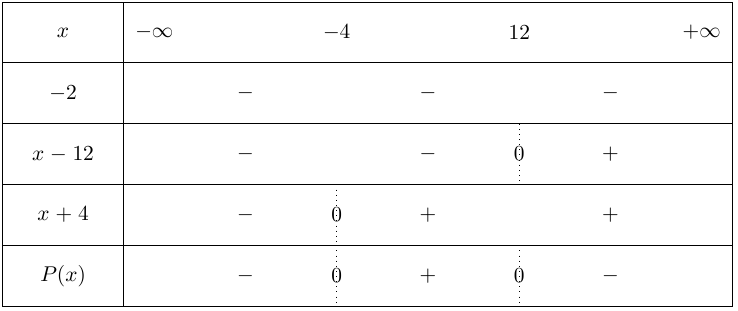
L'ensemble des solutions de \(P(x) \geq 0\) est \(S=[-4 ;12]\)
Attention au facteur "-2".
Question 4
Déterminer la forme canonique de \(P\).
Pour tout réel \(x\) :
\( \begin{align*} P(x) =-2x^2+16x+96 & \Leftrightarrow P(x) = -2(x^2-8x)+96 \\ &\Leftrightarrow P(x) = -2[(x-4)^2-4^2]+96 \\ &\Leftrightarrow P(x) = -2(x-4)^2+32+96 \\ &\Leftrightarrow P(x) = -2(x-4)^2+128 \end{align*} \)
En conclusion : pour tout réel \(x\), la forme canonique de \(P\) est \(P(x) = -2(x-4)^2+128\)
Factorisez par \(-2\) en faisant attention aux signes.
Faites apparaître une identité remarquable.
Question 5
Établir le tableau de variations de \(P\) à l'aide de sa forme canonique.
Comme \(a = - 2\) alors \(a < 0\) et les branches de la parabole \(C_P\) sont tournées vers le bas.
\(P\) est donc croissante puis décroissante.
La forme canonique nous donne les coordonnées du minimum : \((4 ; 128)\).
On en déduit le tableau des variations suivant :
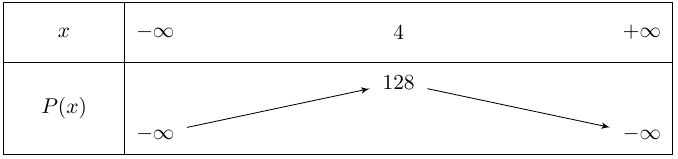
Quelle est alors l'allure de la parabole et donc quelles sont les variations de \(P\) ?
En quel point les variations changent-elles ?
Question 6
Soit \(D\) la droite d'équation \(y = 4x + p\) où \(p\) désigne un réel quelconque. Discuter, suivant les valeurs de \(p\), le nombre de points d'intersection éventuels entre \(C_P\) et \(D\).
Déterminer les points d'intersection de \(C_P\) et \(D\) c'est résoudre l'équation \(P(x) = 4x + p\).
Pour tout réel \(x\) on a :
\( \begin{align*} P(x) = 4x + p &\Leftrightarrow -2x^2+16x+96=4x+p\\ &\Leftrightarrow -2x^2+12x+96-p=0 \end{align*}\)
Soit \(\Delta\) le discriminant de ce trinôme avec \(a = - 2 \ ; b = 12\) et \(c = 96 - p\).
\(\Delta= 12^2 - 4 \times (-2) \times(96-p)\)
Soit \(\Delta = 144+8(96-p)\)
Donc \(\Delta = 912 - 8p \)
On va distinguer le signe de \(\Delta\) selon la valeur de \(p\) :
\(\Delta < 0 \Leftrightarrow 912 - 8p < 0 \Leftrightarrow - 8p < - 912 \Leftrightarrow p > 114\)
De même,
\(\Delta > 0 \Leftrightarrow p < 114\) et
\(\Delta = 0 \Leftrightarrow p = 114\)
Conclusion :
- Si \(p > 114\) alors \(\Delta < 0\), et donc l'équation \(P(x) = 4x + p\) n'admet aucune solution. \(C_P\) et \(D\) n'ont alors aucun point d'intersection.
- Si \(p < 114\) alors \(\Delta > 0\), et donc l'équation \(P(x) = 4x + p\) admet deux solutions. \(C_P\) et \(D\) ont alors deux points d'intersection.
- Si \(p = 114\) alors \(\Delta = 0\), et donc l'équation \(P(x) = 4x + p\) admet une solution. \(C_P\) et \(D\) ont alors un seul point d'intersection.
Calculer \(\Delta\) en fonction de \(p\).
Chercher le signe de \(\Delta\) selon la valeur de \(p\).
